题目内容
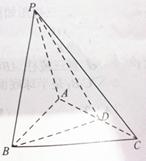
在如图所示的几何体中,四边形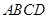 是正方形,
是正方形,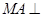 平面
平面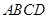 ,
,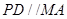 ,
,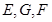 分别为
分别为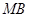 ,
,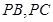 的中点,且
的中点,且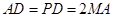 .
.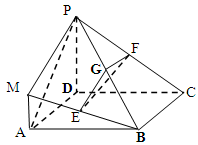
(Ⅰ)求证:平面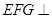 平面
平面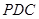 ;
;
(Ⅱ)求三棱锥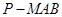 与四棱锥
与四棱锥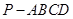 的体积之比.
的体积之比.
(Ⅰ)见解析;(Ⅱ) .
.
解析试题分析:(Ⅰ)要证面面垂直则先证线面垂直,此题由已知条件先证明 ,再由在三角形
,再由在三角形 中,
中, ,得
,得 ,从而
,从而 ,易知
,易知 ;(Ⅱ)根据题意易知四棱锥体积,三棱锥
;(Ⅱ)根据题意易知四棱锥体积,三棱锥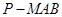 可以把
可以把 作为底面,
作为底面, 即为高,可得体积比.
即为高,可得体积比.
试题解析:(Ⅰ)
 ,
, 平面
平面 ,
,
又 平面
平面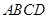 ,
, ,
, ,
, 又
又 , 4分
, 4分
在 ,
, ,
, ,又
,又 . 6分
. 6分
(Ⅱ) ,则
,则 ,
, , 8分
, 8分
依题意知 ,
, ,
,
 . 12分
. 12分
考点:1、面面垂直的判定定理;2、三棱锥和四棱锥的体积公式.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
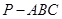 中,
中, ,
,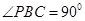 ,D为AC的中点,
,D为AC的中点,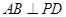 .
.
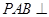 平面
平面 ;
; 的体积为3,求
的体积为3,求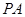 .
.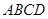 与直角梯形
与直角梯形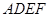 所在平面互相垂直,
所在平面互相垂直,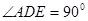 ,
, ,
,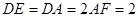 .
.
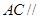 平面
平面 ;
;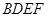 的体积.
的体积. 中,
中,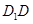
 底面
底面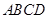 ,
, ,
,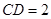 ,
,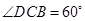 .
.
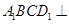 平面
平面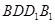 ;
;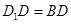 ,求四棱锥
,求四棱锥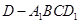 的体积.
的体积.
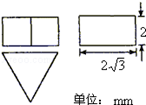
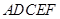 (如图1),
(如图1),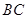 为对称轴,
为对称轴,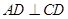 ,
,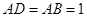 ,
,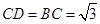 ,将此图形沿
,将此图形沿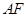 、
、 得到几何体(如图2).
得到几何体(如图2).

 ;
; 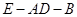 的余弦值.
的余弦值.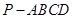 中,底面
中,底面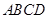 为矩形,
为矩形,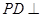 平面
平面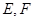 分别是
分别是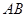 和
和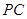 的中点.
的中点.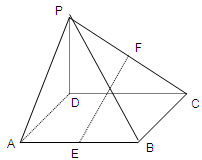
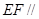 平面
平面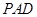 ;
;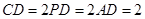 , 四棱锥
, 四棱锥