题目内容
已知三棱柱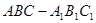 ,底面三角形
,底面三角形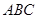 为正三角形,侧棱
为正三角形,侧棱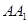
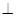 底面
底面 ,
,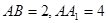 ,
,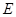 为
为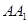 的中点,
的中点,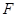 为
为 中点.
中点.
(Ⅰ)求证:直线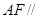 平面
平面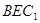 ;
;
(Ⅱ)求点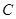 到平面
到平面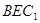 的距离.
的距离.
(Ⅰ)取 的中点为
的中点为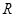 ,连接
,连接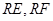 ,
,
推出 ,
,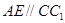 ,且
,且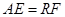 ,
,
利用四边形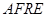 为平行四边形,得到
为平行四边形,得到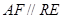 ,
,
所以直线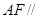 平面
平面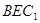 .
.
(Ⅱ)点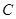 到平面
到平面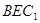 的距离为
的距离为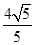 .
.
解析试题分析:(Ⅰ)取 的中点为
的中点为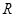 ,连接
,连接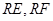 ,
,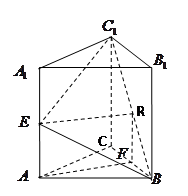
因为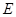 为
为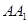 的中点,
的中点,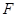 为
为 中点,
中点,
所以 ,
,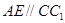 ,且
,且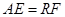 ,
,
所以四边形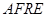 为平行四边形, 所以
为平行四边形, 所以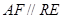 ,
,
又因为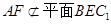 ,
, 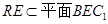
所以直线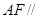 平面
平面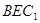 .
.
(Ⅱ)由已知得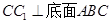 ,所以
,所以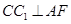 ,
,
因为底面三角形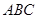 为正三角形,
为正三角形,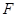 为
为 中点,
中点,
所以 , 所以
, 所以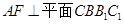 ,
,
由(Ⅰ)知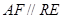 ,所以
,所以 ,
,
因为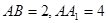 ,所以
,所以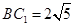 ,
,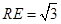 ,
,
设点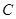 到平面
到平面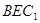 的距离为
的距离为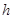 ,由等体积法得
,由等体积法得 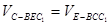 ,
,
所以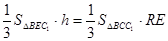 ,得
,得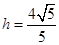 ,
,
即点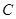 到平面
到平面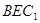 的距离为
的距离为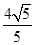 .
.
考点:正三棱柱的几何特征,平行关系,垂直关系,体积计算,距离计算。
点评:中档题,立体几何问题中,平行关系、垂直关系,角、距离、面积、体积等的计算,是常见题型,基本思路是将空间问题转化成为平面问题,利用平面几何知识加以解决。要注意遵循“一作,二证,三计算”。本题计算距离时,应用了“等体积法”,在几何体不十分规则时,经常用到。

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目

 中,
中,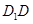
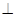 底面
底面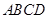 ,
, ,
,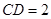 ,
,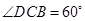 .
.
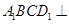 平面
平面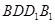 ;
;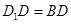 ,求四棱锥
,求四棱锥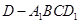 的体积.
的体积.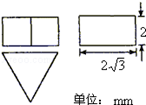
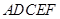 (如图1),
(如图1),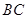 为对称轴,
为对称轴,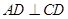 ,
,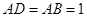 ,
,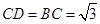 ,将此图形沿
,将此图形沿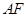 、
、 得到几何体(如图2).
得到几何体(如图2).

 ;
; 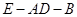 的余弦值.
的余弦值. 中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 为
为 的中点,已知
的中点,已知 ,
,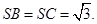
 ;
;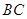 上求一点
上求一点 ,使
,使 平面
平面 ;
; 的体积.
的体积.
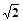 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。
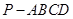 中,底面
中,底面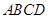 为平行四边形,
为平行四边形,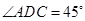 ,
,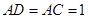 ,
,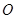 为
为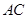 中点,
中点,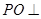 平面
平面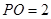 ,
,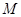 为
为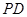 中点.
中点.
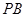 //平面
//平面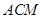 ;
; 平面
平面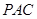 ;
;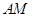 与平面
与平面