题目内容
(本小题满分10分)从某校高三年级800名学生中随机抽取50名测量身高.据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果分成八组得到的频率分布直方图如下:

(1)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少;
(2)在样本中,若学校决定身高在185cm以上的学生中随机抽取2名学生接受某军校考官进行 面试,求:身高在190cm以上的学生中至少有一名学生接受面试的概率.
(1)144;(2)0.7
【解析】
试题分析:(1)由频率分布直方图可知,样本中身高介于185cm~190cm的频率为:
1-(0.008+0.016+0.04+0.04+0.06+0.016+0.008)×5=0.06
∴样本中身高介于在180cm以上的频率为0.06+0.016×5+0.008×5=0.18
∴800名学生中身高在180cm以上的人数为:0.18×800=144人.
(2)样本中,身高介于185cm~190cm的学生人数0.06×50=3人,身高介于190cm~195cm的学生人数为0.04×50=2人.
∴“身高在185cm以上的学生5人中随机抽取2名学生”的基本事件数共10种,
其中抽取的2名学生中“身高在190cm以上的学生中至少有一名学生”的基本事件数有7种.∴所求事件的概率为P=0.7
考点:本题考查频率分布直方图,古典概型的概率
点评:解决本题的关键是掌握在频率分布直方图中,小长方形的面积表示频率,以及

练习册系列答案
相关题目
 中,侧棱垂直底面,
中,侧棱垂直底面, ,
, ,D是棱
,D是棱 的中点.
的中点.
 平面
平面 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. ,焦点坐标为
,焦点坐标为 和
和 的双曲线
的双曲线 ,准线方程为
,准线方程为 的椭圆
的椭圆 轴的正半轴上,焦点到准线的距离为4的抛物线
轴的正半轴上,焦点到准线的距离为4的抛物线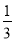 ,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.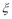 x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A).
x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A). 是⊙
是⊙ 的直径,
的直径, 是弦,∠BAC的平分线
是弦,∠BAC的平分线 交⊙
交⊙ 于
于 ,
, 交
交 延长线于点
延长线于点 ,
, 交
交 于点
于点 .
.
 是⊙
是⊙ 的切线;
的切线; ,求
,求 的值.
的值. 对任意
对任意 恒成立,则实数x的取值范围是( )
恒成立,则实数x的取值范围是( )  B.
B.
 D.
D.
 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C.  D.
D. 
 是定义域为R的奇函数,且当
是定义域为R的奇函数,且当 时,
时, .则函数
.则函数 的零点的个数为( )
的零点的个数为( ) ,则关于
,则关于 的不等式
的不等式 的解集是( )
的解集是( ) B.
B. C.
C. D.
D.