题目内容
18.在△ABC中,若AB=3,AC=4,|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,则$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BC}|}$的值为$\frac{12}{5}$.分析 如图所示,可得平行四边形ABDC是矩形.利用直角三角形的边角关系即可得出.
解答 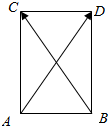 解:如图所示,设$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$,
解:如图所示,设$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$,
∴四边形ABDC是平行四边形
∵|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,
∴平行四边形ABDC是矩形,
∴|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|=$\sqrt{{3}^{2}+{4}^{2}}$=5,
在Rt△ABC中,cos∠ABC=$\frac{4}{5}$,
∴$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BC}|}$=$\frac{3×5×\frac{4}{5}}{5}$=$\frac{12}{5}$,
故答案为:$\frac{12}{5}$.
点评 本题考查了向量的平行四边形法则、矩形的定义、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.营养师要为儿童预定午餐和晚餐,已知一个单位的午餐含12个单位的碳税化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含有8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C,另外,这两餐需要的营养中至少含有64个单位的碳水化合物,42个单位的蛋白质和54个维生素C.
(Ⅰ)根据已知数据填写如表:
(Ⅱ)已知一个单位的午餐,晚餐的费用分别是4元和5元,若预定x个单位的午餐和y个单位的晚餐,共花费z元,请列出满足上述营养要求的不等式组及目标函数;
(Ⅲ)在(Ⅱ)的条件下,并且花费最少,应分别预定多少个单位的午餐和晚餐?
(Ⅰ)根据已知数据填写如表:
| 营养成分 | 碳水化合物/单位 | 蛋白质/单位 | 维生素C/单位 |
| 午餐 | |||
| 晚餐 |
(Ⅲ)在(Ⅱ)的条件下,并且花费最少,应分别预定多少个单位的午餐和晚餐?
13.下列有关命题的说法错误的是( )
| A. | 若“p∨q”为假命题,则p,q均为假命题 | |
| B. | “x=1”是“x≥1”的充分不必要条件 | |
| C. | 若命题p:?x0∈R,x${\;}_{0}^{2}$≥0,则命题¬p:?x∈R,x2<0 | |
| D. | “sinx=$\frac{1}{2}$”的必要不充分条件是“x=$\frac{π}{6}$” |
10.已知函数f(x)=(x2+x)(x2+ax+b),若对?x∈R,均有f(x)=f(2-x),则f(x)的最小值为( )
| A. | -$\frac{9}{4}$ | B. | -$\frac{35}{16}$ | C. | -2 | D. | 0 |
8.已知数列{an}满足a1=1,若n为奇数时,an+1=2an+1;若n为偶数时,an+1=an+n.则该数列的前7项和为( )
| A. | 103 | B. | 102 | C. | 100 | D. | 98 |