题目内容
3.函数f(x)=sin(x+$\frac{π}{4}$)cos(x+$\frac{π}{4}$)-sin2x-ln|x|+$\frac{1}{2}$的零点个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据条件先化简函数f(x),利用函数与方程的关系转化为两个函数的交点个数问题,利用数形结合进行求解即可.
解答 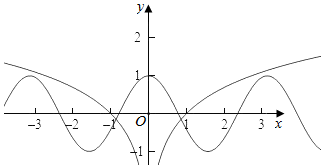 解:f(x)=sin(x+$\frac{π}{4}$)cos(x+$\frac{π}{4}$)-sin2x-ln|x|+$\frac{1}{2}$=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)-$\frac{1-cos2x}{2}$-ln|x|+$\frac{1}{2}$=cos2x-ln|x|,
解:f(x)=sin(x+$\frac{π}{4}$)cos(x+$\frac{π}{4}$)-sin2x-ln|x|+$\frac{1}{2}$=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)-$\frac{1-cos2x}{2}$-ln|x|+$\frac{1}{2}$=cos2x-ln|x|,
由f(x)=cos2x-ln|x|=0得cos2x=ln|x|,
分别作出函数y=cos2x和y=ln|x|的图象如图:
则由图象知两个函数有2个交点,
即函数f(x)的零点个数为2个,
故选:C.
点评 本题主要考查方程根的个数的判断,利用三角函数的公式先化简函数f(x),利用函数与方程的关系转化为两个函数的图象的交点个数问题是解决本题的关键.

练习册系列答案
相关题目
15.如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依此规律A(15,2)表示为( )


| A. | $\frac{29}{42}$ | B. | $\frac{7}{10}$ | C. | $\frac{17}{24}$ | D. | $\frac{73}{102}$ |