题目内容
已知函数f(x)=x3+(a-1)x+1
(1)若f(x)在R上递增,求a的取值范围;
(2)若f(x)在(-1,1)上递减,求a的取值范围;
(3)若f(x)在(-1,1)上不单调,求a的取值范围;
(4)若(-1,1)为f(x)的递减区间,求a的取值范围.
(1)若f(x)在R上递增,求a的取值范围;
(2)若f(x)在(-1,1)上递减,求a的取值范围;
(3)若f(x)在(-1,1)上不单调,求a的取值范围;
(4)若(-1,1)为f(x)的递减区间,求a的取值范围.
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)先求出函数的导数,得到a≥-3x2+1在x∈R时恒成立,从而求出a的范围;
(2)由f′(x)≤0在(-1,1)上恒成立得到不等式,解出即可求出a的范围;
(3)若f(x)在(-1,1)上不单调,则
,解出即可求出a的范围;
(4)若(-1,1)为f(x)的递减区间,则±1为f′(x)=3x2+a-1=0的两根,解出即可求出a值.
(2)由f′(x)≤0在(-1,1)上恒成立得到不等式,解出即可求出a的范围;
(3)若f(x)在(-1,1)上不单调,则
|
(4)若(-1,1)为f(x)的递减区间,则±1为f′(x)=3x2+a-1=0的两根,解出即可求出a值.
解答:
解:∵f(x)=x3+(a-1)x+1,
∴f′(x)=3x2+a-1,
(1)若f(x)在R上递增,则f′(x)≥0恒成立,
即a≥-3x2+1在x∈R时恒成立.
而-3x2+1≤1,
∴a≥1,
∴实数a的取值范围是[1,+∞).
(2)由条件f′(x)≤0,
即a≤-3x2+1在x∈(-1,1)时恒成立.
∵x∈(-1,1)时,3x2∈[0,3),
∴只要a≤-2即可,
∴实数a的取值范围是(-∞,-2].
(3)若f(x)在(-1,1)上不单调,
则
,
即
,
解得:-2<a<1,
(4)若(-1,1)为f(x)的递减区间,
则±1为f′(x)=3x2+a-1=0的两根,
解得:a=-2.
∴f′(x)=3x2+a-1,
(1)若f(x)在R上递增,则f′(x)≥0恒成立,
即a≥-3x2+1在x∈R时恒成立.
而-3x2+1≤1,
∴a≥1,
∴实数a的取值范围是[1,+∞).
(2)由条件f′(x)≤0,
即a≤-3x2+1在x∈(-1,1)时恒成立.
∵x∈(-1,1)时,3x2∈[0,3),
∴只要a≤-2即可,
∴实数a的取值范围是(-∞,-2].
(3)若f(x)在(-1,1)上不单调,
则
|
即
|
解得:-2<a<1,
(4)若(-1,1)为f(x)的递减区间,
则±1为f′(x)=3x2+a-1=0的两根,
解得:a=-2.
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
相关题目
已知cos(
+a)=
,-
<a<0,则sin2α的值是( )
| 5π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设全集U={x|log2x<3},A={x|1<2x<32},则CUA=( )
| A、(-∞,0]∪[5,8) |
| B、(-∞,0]∪(5,8) |
| C、[5,8) |
| D、(5,8) |
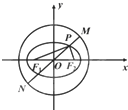 如图,已知椭圆C:
如图,已知椭圆C: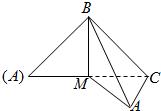 如图,等腰直角△ABC中,已知AB=BC=2,M为AC中点,沿BM将它折成二面角,折后A,C间的距离为
如图,等腰直角△ABC中,已知AB=BC=2,M为AC中点,沿BM将它折成二面角,折后A,C间的距离为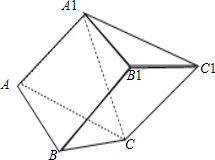 已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2