题目内容
直线l过点A(-2,3),且点B(1,-1)到该直线l的距离为3,则直线l的方程为 .
考点:点到直线的距离公式
专题:直线与圆
分析:当直线l无斜率时,方程为x+2=0,满足题意;当直线l有斜率时,设方程为y-3=k(x+2),由点到直线的距离公式可k值,可得方程,综合可得.
解答:
解:当直线l无斜率时,方程为x=-2即x+2=0,显然满足点B(1,-1)到该直线l的距离为3;
当直线l有斜率时,设方程为y-3=k(x+2)即kx-y+2k+3=0,
由题意可得
=3,解得k=-
,
∴直线l的方程为y-3=-
(x+2),化为一般式可得7x+24y-58=0
故答案为:x+2=0或7x+24y-58=0
当直线l有斜率时,设方程为y-3=k(x+2)即kx-y+2k+3=0,
由题意可得
| |k+1+2k+3| | ||
|
| 7 |
| 24 |
∴直线l的方程为y-3=-
| 7 |
| 24 |
故答案为:x+2=0或7x+24y-58=0
点评:本题考查点到直线的距离公式,涉及分类讨论的思想,属基础题.

练习册系列答案
相关题目
一个正三棱柱的正视图是正方形,且它的外接球的表面积等于
,则这个正三棱柱的底面边长为( )
| 25π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
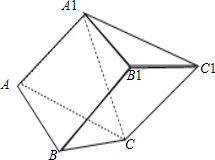 已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知斜三棱柱ABC-A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2