题目内容
13.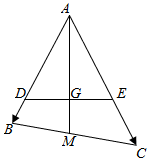 过△ABC的重心G任作一条直线分别交AB,AC于点D、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
过△ABC的重心G任作一条直线分别交AB,AC于点D、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.(1)用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{AG}$;
(2)若$\overrightarrow{AD}$=x$\overrightarrow{AB}$,$\overrightarrow{AE}$=y$\overrightarrow{AC}$,且xy≠0,求$\frac{1}{x}$+$\frac{1}{y}$的值.
分析 (1)根据重心的性质及向量加法的平行四边形法则便可得出$\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b})$;
(2)由条件即可得到$\overrightarrow{AB}=\frac{1}{x}\overrightarrow{AD},\overrightarrow{AC}=\frac{1}{y}\overrightarrow{AE}$,这样带入$\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$便可得出$\overrightarrow{AG}=\frac{1}{3x}\overrightarrow{AD}+\frac{1}{3y}\overrightarrow{AE}$,而由图看出D,G,E三点共线,从而便可得出$\frac{1}{3x}+\frac{1}{3y}=1$,这样即可求出$\frac{1}{x}+\frac{1}{y}$的值.
解答 解:(1)G为△ABC的重心;
∴$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b})$;
(2)根据条件,$\overrightarrow{AB}=\frac{1}{x}\overrightarrow{AD},\overrightarrow{AC}=\frac{1}{y}\overrightarrow{AE}$;
∴$\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$
=$\frac{1}{3}(\frac{1}{x}\overrightarrow{AD}+\frac{1}{y}\overrightarrow{AE})$
=$\frac{1}{3x}\overrightarrow{AD}+\frac{1}{3y}\overrightarrow{AE}$;
又D,G,E三点共线;
∴$\frac{1}{3x}+\frac{1}{3y}=1$;
∴$\frac{1}{x}+\frac{1}{y}=3$.
点评 考查三角形重心的概念及重心的性质,向量的数乘运算,以及向量加法的平行四边形法则,知道三点A,B,C共线的充要条件:$\overrightarrow{OB}=x\overrightarrow{OA}+y\overrightarrow{OC}$,且x+y=1.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
