题目内容
8.如图所示的伪代码运行后输出的结果为23,9.
分析 分析程序中各变量各语句的作用,再根据流程图所示的顺序可知:该程序的作用是利用循环计算并输出变量S,I的值,模拟程序的运行,对程序运行过程中各变量的值进行分析,不难得到输出结果.
解答 解:模拟执行程序,可得
I=1
满足条件S≤21,执行循环体,I=3,S=9,I=2
满足条件S≤21,执行循环体,I=4,S=11,I=3
满足条件S≤21,执行循环体,I=5,S=13,I=4
满足条件S≤21,执行循环体,I=6,S=15,I=5
满足条件S≤21,执行循环体,I=7,S=17,I=6
满足条件S≤21,执行循环体,I=8,S=19,I=7
满足条件S≤21,执行循环体,I=9,S=21,I=8
满足条件S≤21,执行循环体,I=10,S=23,I=9
不满足条件S≤21,退出循环,输出S,I的值为23,9.
故答案为:23,9.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
18.已知z是纯虚数,i为虚数单位,$\frac{z+2}{1-i}$在复平面内所对应的点在实轴上,那么z等于( )
| A. | 2i | B. | i | C. | -i | D. | -2i |
16.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个顶点作一条渐近线的垂线,垂足为P,记以双曲线的实轴为长轴且过点P的椭圆的离心率为e1,双曲线的离心率为e2,则$\frac{1}{{e}_{1}^{2}}$-$\frac{1}{{e}_{2}^{2}}$=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
20.双曲线中,焦点为F1(-3,0),F2(3,0),实半轴a=2,则双曲线的方程是( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 |
17.执行如图所示的程序框图,若输出的值为-5,则判断框中可以填入的条件为( )

| A. | z>10? | B. | z≤10? | C. | z>20? | D. | z≤20? |
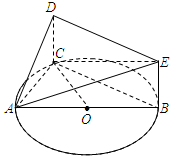 如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.
如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.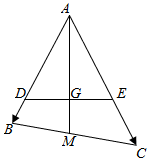 过△ABC的重心G任作一条直线分别交AB,AC于点D、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
过△ABC的重心G任作一条直线分别交AB,AC于点D、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.