题目内容
2.若数列{an}的通项公式是an=(-1)n•(3n-2),求数列{an}的前n项和.分析 对n分类讨论,分组求和即可得出.
解答 解:∵an=(-1)n•(3n-2),
∴n=2k(k∈N*)时,T2k=(-1+4)+(-7+10)+…+[-3(2k-1)+2+3×2k-2]
=3k=$\frac{3n}{2}$.
n=2k-1(k∈N*)时,T2k-1=-1+(4-7)+(10-13)+…+[3(2k-3)-2-3×(2k-1)+2]
=-1-3×(k-1)=-3k+2=$\frac{1-3n}{2}$.
∴数列{an}的前n项和Tn=$\left\{\begin{array}{l}{\frac{3n}{2},n=2k}\\{\frac{1-3n}{2},n=2k-1}\end{array}\right.$,k∈N*.
点评 本题考查了递推关系、等差数列的通项公式及其前n项和公式、分组求和方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.函数y=2cos2(x+$\frac{π}{4}$)-1的一个单调递减区间是( )
| A. | ($\frac{π}{2}$,$\frac{3π}{2}$) | B. | ($\frac{π}{4}$,$\frac{3π}{4}$) | C. | (-$\frac{π}{2}$,$\frac{π}{2}$) | D. | (-$\frac{π}{4}$,$\frac{π}{4}$) |
17.执行如图所示的程序框图,若输出的值为-5,则判断框中可以填入的条件为( )

| A. | z>10? | B. | z≤10? | C. | z>20? | D. | z≤20? |
14.非空集合A={(x,y)$\left\{\begin{array}{l}{ax-2y+8≥0}\\{x-y-1≤0}\\{2x+ay-2≤0}\end{array}\right.$},当(x,y)∈A时,对任意实数m,目标函数z=x+my的最大值和最小值至少有一个不存在,则实数a的取值范围是( )
| A. | (-∞,2) | B. | [0,2) | C. | [2,+∞) | D. | (2,+∞) |
11.将函数f(x)=sin(x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位后的图象关于y轴对称,则函数f(x)在[0,$\frac{π}{2}$]上的最小值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
11.如图程序运行后,得到的a,b,c分别为( )


| A. | 2,3,2 | B. | 2,3,1 | C. | 3,2,1 | D. | 3,2,3 |
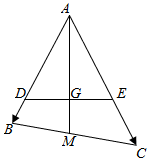 过△ABC的重心G任作一条直线分别交AB,AC于点D、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
过△ABC的重心G任作一条直线分别交AB,AC于点D、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.