题目内容
5.双曲线的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{6}}{2}$,斜率为1的直线l经过M(2,0)且此双曲线与l交于A、B两点,若|AB|=4$\sqrt{3}$,求双曲线的方程.分析 由离心率公式可得c=$\frac{\sqrt{6}}{2}$a,b=$\sqrt{{c}^{2}-{a}^{2}}$=$\frac{\sqrt{2}}{2}$a,设出直线AB方程,然后联立双曲线的方程消去y得x的方程,利用|AB|=4$\sqrt{3}$,建立方程,即可求a=$\sqrt{2}$,求得b,即可得到所求双曲线的方程.
解答 解:设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$,即c=$\frac{\sqrt{6}}{2}$a,b=$\sqrt{{c}^{2}-{a}^{2}}$=$\frac{\sqrt{2}}{2}$a,
设直线方程为y=x-2,
将b=$\frac{\sqrt{2}}{2}$a代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,即有x2-2y2=a2,
整理可得x2-8x+8+a2=0,
设A(x1,y1),B(x2,y2),
可得x1+x2=8,x1x2=8+a2,
|AB|=$\sqrt{1+1}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\sqrt{64-4(8+{a}^{2})}$=4$\sqrt{3}$,
解得a=$\sqrt{2}$,即有b=1,
则双曲线的方程为$\frac{{x}^{2}}{2}$-y2=1.
点评 本题考查双曲线的标准方程的求法,注意运用直线方程和双曲线的方程联立,运用韦达定理和弦长公式,考查运算能力,属于中档题.

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 |
| A. | ($\frac{π}{2}$,$\frac{3π}{2}$) | B. | ($\frac{π}{4}$,$\frac{3π}{4}$) | C. | (-$\frac{π}{2}$,$\frac{π}{2}$) | D. | (-$\frac{π}{4}$,$\frac{π}{4}$) |

| A. | z>10? | B. | z≤10? | C. | z>20? | D. | z≤20? |
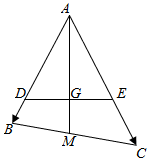 过△ABC的重心G任作一条直线分别交AB,AC于点D、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
过△ABC的重心G任作一条直线分别交AB,AC于点D、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.