题目内容

在△ABC中，
AM
=
1
4
AB
+m•
AC
，向量
AM
的终点M在△ABC的内部（不含边界），则实数m的取值范围是
 
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，设
AD
=
1
4
AB
，过点D作DE∥AC交BC于点E．由
AM
=
1
4
AB
+m•
AC
，可知点M在线段DE上（不含点D，E），借助于点D，E即可得出．
解答： 解：如图所示，设
AD
=
1
4
AB
，过点D作DE∥AC交BC于点E．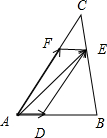
∵
AM
=
1
4
AB
+m•
AC
，可知点M在线段DE上（不含点D，E）
当点M取点D时，
AM
=
1
4
AB
，可得m=0，而M在△ABC的内部（不含边界），因此m＞0．
当点M取点E时，
AM
=
1
4
AB
+
3
4
AC
，此时可得m=
3
4
，而M在△ABC的内部（不含边界），因此m＜
3
4
．
∴0＜m＜
3
4
．
故答案为：0＜m＜
3
4
．
点评：本题考查了向量的平行四边形法则、共面向量的基本定理，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn，若Sk=2，S3k=12，则S4k=
 
．
已知函数f（x）与g（x）的图象关于直线x=2对称，若f（x）=4x-15，则不等式
g(x)
x2-1
≥0的解集是
 
．
已知集合A={x|x＜5，x∈N}，将集合A用列举法表示为
 
．
已知△ABC中，AB=4
3
，AC=2
3
，AD为BC边上的中线，且∠BAD=30°，则BC=
 
．
已知函数y=f（x）是定义在R上的奇函数，且当x＜0时，f（x）=2x+1，则f（3-log23）=
 
．
边长为a的正三角形，用斜二测画法得到其直观图，则该直观图的面积为
 
．
关于工序流程图的说法错误的是（　　）
A、工序流程图又称统筹图
B、开始时工序流程图可以画得粗疏，然后再对每一框细化
C、工序流程图中的平行四边形框表示一道工序
D、工序流程图中两相邻工序之间用流程线相连
已知函数f（x）=lnx-
1
x
+2（x＞0），则函数f（x）的零点个数是（　　）
A、0B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网