题目内容
12.将函数$y=sin({2x-\frac{π}{6}})$的图象向右平移$\frac{π}{4}$个单位,所得函数图象的一条对称轴方程为( )| A. | $x=\frac{π}{12}$ | B. | $x=\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{12}$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,求出所得函数图象的一条对称轴方程.
解答 解:将函数$y=sin({2x-\frac{π}{6}})$的图象向右平移$\frac{π}{4}$个单位,可得y=sin(2x-$\frac{π}{2}$-$\frac{π}{6}$)=sin(2x-$\frac{2π}{3}$)的图象,
令2x-$\frac{2π}{3}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{7π}{12}$,k∈Z,
再令k=-1,可得所得函数图象的一条对称轴方程为x=$\frac{π}{12}$,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
4. 已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.
已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.
(1)求异面直线BP和AD所成角的余弦值;
(2)求点E到平面PAD的距离.
 已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.
已知球内接正四棱锥P-ABCD的高为3,AC,BC相交于O,球的表面积为$\frac{169π}{9}$,若E为PC中点.(1)求异面直线BP和AD所成角的余弦值;
(2)求点E到平面PAD的距离.
9. 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )| A. | ∁U(A∩B) | B. | ∁U(A∪B) | C. | (A∪B)∩(∁U(A∩B)) | D. | ((∁UA)∩B)∩(∁UB)∩A) |
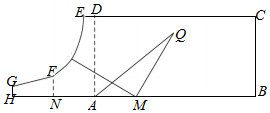 如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).
如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).