题目内容
解下列方程:
(1)x -
=
(2)2x
-1=15
(3)log2(2x+1)=log2(x2-2)
(4)lg
=lg(x-1).
(1)x -
| 1 |
| 3 |
| 1 |
| 8 |
(2)2x
| 3 |
| 4 |
(3)log2(2x+1)=log2(x2-2)
(4)lg
| x-1 |
考点:指、对数不等式的解法
专题:函数的性质及应用
分析:利用指数幂和对数的运算性质化简所给的式子,从而求得方程的解.
解答:
解:(1)由 x -
=
,可得
=
,故有
=8,求得 x=83.
(2)由 2x
-1=15,可得 x
=8,即 x=8
=24=16.
(3)由 log2(2x+1)=log2(x2-2)可得2x+1=x2-2>0,求得x=1+
.
(4)由lg
=lg(x-1)可得
=x-1,∴x-1=1,解得x=2.
| 1 |
| 3 |
| 1 |
| 8 |
| 1 | |||
|
| 1 |
| 8 |
| 3 | x |
(2)由 2x
| 3 |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
(3)由 log2(2x+1)=log2(x2-2)可得2x+1=x2-2>0,求得x=1+
| 2 |
(4)由lg
| x-1 |
| x-1 |
点评:本题主要考查指数方程、对数方程的解法,指数幂和对数的运算性质的应用,体现了等价转化的数学思想,属于基础题.

练习册系列答案
相关题目

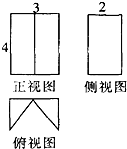 如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,则该几何体的体积是
如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,则该几何体的体积是