题目内容
11. 某重点高中拟把学校打造成新型示范高中,为此制定了很多新的规章制度,新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问題5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85)第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲、乙、丙上分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对新规取章制度作深入学习.
某重点高中拟把学校打造成新型示范高中,为此制定了很多新的规章制度,新规章制度实施一段时间后,学校就新规章制度的认知程度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问題5分,调查结束后,发现这100名学生的成绩都在[75,100]内,按成绩分成5组:第1组[75,80),第2组[80,85)第3组[85,90),第4组[90,95),第5组[95,100],绘制成如图所示的频率分布直方图,已知甲、乙、丙上分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对新规取章制度作深入学习.(1)求这100人的平均得分(同-组数据用该区间的中点值作代表);
(2)求第3,4,5组分别选取的人数;
(3)若甲、乙、丙都被选取对新规章制度作深人学习,之后要从这6人随机选取人2再全面考查他们对新规章制度的认知程度,求甲、乙、丙这3人至多有一人被选取的概率.
分析 (1)利用频率分布直方图能求出这100人的平均得分.
(2)第3组的人数为30,第4组的人数为20,第5组的人数为10,共有60人,由此能示出用分层抽样在这三个组选取的人数.
(3)记其他人为、丁、戊、己,利用列举法能求出甲、乙、丙这3人至多有一人被选取的概率.
解答 解:(1)这100人的平均得分为:
$\overline x=5×({\frac{75+80}{2}×0.01+\frac{80+85}{2}×0.07+\frac{85+90}{2}×0.06+\frac{90+95}{2}×0.04+\frac{95+100}{2}×0.02})=87.25$.
(2)第3组的人数为0.06×5×100=30,
第4组的人数为0.04×5×100=20,
第5组的人数为0.02×5×100=10,故共有60人,
∴用分层抽样在这三个组选取的人数分别为:3,2,1.
(3)记其他人为、丁、戊、己,
则所有选取的结果为(甲、乙)、(甲、丙)、(甲、丁)、(甲、戊)、(甲、己)、
(乙、丙)、(乙、丁)、(乙、戊)、(乙、己 )、(丙、丁)、(丙、戊)、(丙、己)、
(丁、戊)、(丁、己 )、(戊、己)共15种情况,
其中甲、乙、丙这3人至多有一人被选取有12种情况,
故甲、乙、丙这3人至多有一人被选取的概率为$P=\frac{12}{15}=\frac{4}{5}$.
点评 本题考查频率分布直方图、分层抽样、古典概型等知识点,解题的关键是列出所有可能的组合,再去根据相关的定义和公式进行求解和计算.

练习册系列答案
相关题目
2.某企业第三年的产量比第一年的产量增加44%,若每年的平均增长率相同(设为x),则以下结论正确的是( )
| A. | x>22% | B. | x<22% | C. | x=22% | D. | 以上都不对 |
6.设向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2\sqrt{2},|{\overrightarrow b}|=\sqrt{2}$,且$\overrightarrow a•\overrightarrow b=1$,则$|{\overrightarrow a-2\overrightarrow b}|$=( )
| A. | $2\sqrt{3}$ | B. | 12 | C. | $2\sqrt{2}$ | D. | 8 |
12.已知向量|$\overrightarrow{a}$|=3,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{2}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{3\sqrt{6}}{2}$,则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
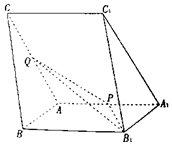 如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.
如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点. 如图,直角梯形OABC中,∠COA=∠OAB=$\frac{π}{2}$,OC=2,OA=AB=1,SO⊥平面OABC,且SO=1,点M为SC的中点.
如图,直角梯形OABC中,∠COA=∠OAB=$\frac{π}{2}$,OC=2,OA=AB=1,SO⊥平面OABC,且SO=1,点M为SC的中点.