题目内容
学校准备从5位报名同学中挑选3人,分别担任2014年江苏省运动会田径、游泳和球类3个不同比赛项目的志愿者.已知其中同学甲不能担任游泳比赛的志愿者,则不同的安排方法共有 种.(结果用数字表示)
考点:计数原理的应用
专题:排列组合
分析:分两类,若选出的3人中没有甲,若选出的3人中有甲,相加即得所求.
解答:
解:若选出的3人中没有甲,方法有
•
•=24种.
若选出的3人中有甲,方法共有
•
=24种,
故不同的安排方法共有24+24=48种,
故答案为:48
| C | 3 4 |
| A | 3 3 |
若选出的3人中有甲,方法共有
| C | 1 2 |
| A | 2 4 |
故不同的安排方法共有24+24=48种,
故答案为:48
点评:本题主要考查排列、组合以及简单计数原理的应用,体现了分类讨论的数学思想,注意把特殊元素与位置综合分析,分类讨论,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
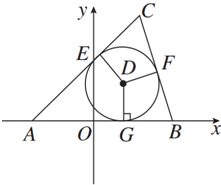 △ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是
△ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是