题目内容
已知圆C:(x+2)2+(y-b)2=3(b>0)过点(-2+
,0),直线l:y=x+m(m∈R).
(1)求b的值;
(2)若直线l与圆C相切,求m的值;
(3)若直线l与圆C相交于M,N两点,且OM⊥ON(O为坐标原点),求实数m的值.
| 2 |
(1)求b的值;
(2)若直线l与圆C相切,求m的值;
(3)若直线l与圆C相交于M,N两点,且OM⊥ON(O为坐标原点),求实数m的值.
考点:圆的切线方程,直线与圆的位置关系
专题:综合题,直线与圆
分析:(1)由题,圆C:(x+2)2+(y-b)2=3(b>0)过点(-2+
,0),代入求b的值;
(2)若直线l与圆C相切,圆心C(-2,1)到直线l的距离等于圆C的半径
,即可求m的值;
(3)先把直线与圆的方程联立消去y,因为OM⊥ON得到x1x2+y1y2=0,然后利用根于系数的关系求出m即可.
| 2 |
(2)若直线l与圆C相切,圆心C(-2,1)到直线l的距离等于圆C的半径
| 3 |
(3)先把直线与圆的方程联立消去y,因为OM⊥ON得到x1x2+y1y2=0,然后利用根于系数的关系求出m即可.
解答:
解:(1)由题,圆C:(x+2)2+(y-b)2=3(b>0)过点(-2+
,0),则
(-2+
+2)2+(0-b)2=3(b>0),…(2分)
解得:b=1 …(4分)
(2)因为直线l与圆C相切,
所以圆心C(-2,1)到直线l的距离等于圆C的半径
即:
=
…(6分)
解得:m=3±
…(7分)
(3)设M(x1,y1)、N(x2,y2),
由直线代入圆的方程,消去y得:2x2+2(m+1)x+m2-2m+2=0,…(8分)
所以x1+x2=-(m+1),x1x2=
,
因为OM⊥ON,所以x1x2+y1y2=0,
所以2x1x2+m(x1+x2)+m2=0
所以m2-3m+2=0,
解得:m=1,或m=2 …(13分)
检验可知:它们满足△>0,
故所求m的值为1或2…(14分)
| 2 |
(-2+
| 2 |
解得:b=1 …(4分)
(2)因为直线l与圆C相切,
所以圆心C(-2,1)到直线l的距离等于圆C的半径
| 3 |
即:
| |-2-1+m| | ||
|
| 3 |
解得:m=3±
| 6 |
(3)设M(x1,y1)、N(x2,y2),
由直线代入圆的方程,消去y得:2x2+2(m+1)x+m2-2m+2=0,…(8分)
所以x1+x2=-(m+1),x1x2=
| m2-2m+2 |
| 2 |
因为OM⊥ON,所以x1x2+y1y2=0,
所以2x1x2+m(x1+x2)+m2=0
所以m2-3m+2=0,
解得:m=1,或m=2 …(13分)
检验可知:它们满足△>0,
故所求m的值为1或2…(14分)
点评:此题是一道直线与圆的方程的综合题,主要考查学生对圆标准方程的认识,会利用根与系数的关系解决数学问题.

练习册系列答案
相关题目
函数 f(x)=sin(ωx+φ)+b的图象如图,则 f(x)的解析式S=f(1)+f(2)+f(3)+…+f(2015)的值分别为( )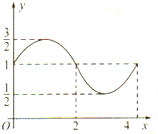

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
在△ABC中,A=30°,a=2,则
的值为( )
| a+b+c |
| sinA+sinB+sinC |
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
 如果输入n=1,那么执行如图中算法的结果是输出
如果输入n=1,那么执行如图中算法的结果是输出