题目内容
已知命题p：存在n∈N，使得2n＞1000，则p的否定为 ．
考点：命题的否定
专题：简易逻辑
分析：利用特称命题的否定是全称命题，写出结果即可．
解答：
解：因为特称命题的否定是全称命题，所以，命题p：存在n∈N，使得2n＞1000，则p的否定为：任意n∈N，都有2n≤1000；
故答案为：任意n∈N，都有2n≤1000．
故答案为：任意n∈N，都有2n≤1000．
点评：本题考查命题的否定特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
“p∨q是假命题”是“p或q为真命题”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f（x）=
的定义域是（ ）
| x2-4 |
| A、（-2，2） |
| B、[-2，2] |
| C、（-∞，-2）∪（2，+∞） |
| D、（-∞，-2]∪[2，+∞） |
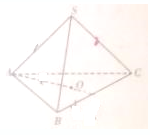如图，在三棱锥S-ABC中，AB=AC，顶点S在底面ABC上的射影是△ABC的重心O，BC=8，AO=2，SA=