Question

【题目】已知f（x）是定义在R上的偶函数，当x≥0时，f（x）=|x﹣1|，若方程f（x）= 有4个不相等的实根，则实数a的取值范围是（ ）
A.（﹣ ，1）
B.（ ，1）
C.（ ，1）
D.（﹣1， ）

Answer 1

【答案】B
【解析】解：设x＜0，则﹣x＞0，

∵当x≥0时，f（x）=|x﹣1|，∴f（﹣x）=|﹣x﹣1|=|x+1|，

∵f（x）是定义在R上的偶函数，∴f（x）=f（﹣x）=|x+1|，

则f（x）= ，即 ，

由f（x）= 得，f2（x）=x+a，

画出函数y=x+a与y=f2（x）的图象，如图所示：

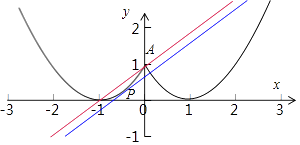
由图知，当直线y=x+a过点A时有三个交点，

且A（1，1），此时a=1，

当直线y=x+a相切与点P时有三个交点，

由图知，y=f2（x）=（x+1）2=x2+2x+1，

则y′=2x+2，令y′=2x+2=1得x= ，则y= ，

此时切点P（ ， ），代入y=x+a得a= ，

∵方程f（x）= 有4个不相等的实根，

∴函数y=x+a与y=f2（x）的图象有四个不同的交点，

由图可得，实数a的取值范围是（ ，1），

故选B．

【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识，掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．