Question

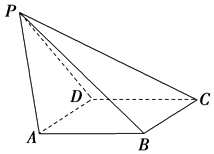
【题目】在棱长为2的正方体内有一四面体A﹣BCD，其中B，C分别为正方体两条棱的中点，其三视图如图所示，则四面体A﹣BCD的体积为（ ）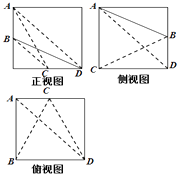

A.
B.2
C.
D.1

Answer 1

【答案】D
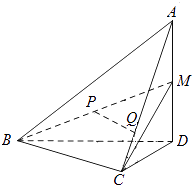
【解析】解：由已知中的三视图，可得A，B，C，D四点位置如下图所示：

∵正方体的棱长为2，故AB=BD=AC=CD= ，AD=2 ，BC= ，
令E为AD的中点，连接BE，CE，
则BE⊥AD，CE⊥AD，
则AD⊥平面BCE，
由勾股定理可得：BE=CE= ，
由海伦公式平面BCE的面积S= ，
又由AD=2 ，
故四面体A﹣BCD的体积V= × ×2 =1，
故选：D
【考点精析】掌握由三视图求面积、体积是解答本题的根本，需要知道求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．