Question

【题目】在正四棱柱ABCD﹣A1B1C1D1中，AA1=2AB，E为棱CC1上的动点．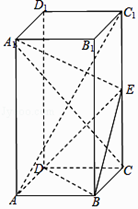
（1）若E为棱CC1的中点，求证：A1E⊥平面BDE；
（2）试确定E点的位置使直线A1C与平面BDE所成角的正弦值是 ．

Answer 1

【答案】
（1）证明：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，

设AA1=2AB=2，E为棱CC1的中点，

则A1（1，0，2），E（0，1，1），B（1，1，0），D（0，0，0），

=（﹣1，1，﹣1）， =（1，1，0）， =（0，1，1），

=﹣1+1=0， =1﹣1=0，

∴A1E⊥DB，A1E⊥DE，

又DB∩DE=D，∴A1E⊥平面BDE

（2）解：C（0，1，0），设E（0，1，t），

则 =（1，1，0）， =（0，1，t）， =（﹣1，1，﹣2），

设平面DBE的法向量 =（a，b，c），

则 ，取a=1，得 =（1，﹣1， ），

∵直线A1C与平面BDE所成角的正弦值是 ．

∴|cos＜ ＞|= = = ，

解得t=1或t= （舍），

∴E是CC1的中点或CE占CC1的 ．

【解析】（1）以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能证明A1E⊥平面BDE．（2）求出平面DBE的法向量，由直线A1C与平面BDE所成角的正弦值是 ．利用向量法能确定E点的位置．
【考点精析】本题主要考查了直线与平面垂直的判定和空间角的异面直线所成的角的相关知识点，需要掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则才能正确解答此题．