题目内容
8.函数y=cos2x-sin2x+2sinxcosx的值域是( )| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [$-\sqrt{2}$,$\sqrt{2}$] | D. | [-2,2] |
分析 将函数进行化简只有一个函数名,结合三角函数的图象和性质即可求函数y的值域;
解答 解:函数y=cos2x-sin2x+2sinxcosx=cos2x+sin2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$).
∴sin(2x+$\frac{π}{4}$)∈[-1,1]
∴函数y=cos2x-sin2x+2sinxcosx的值域为[$-\sqrt{2}$,$\sqrt{2}$].
故选C.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
相关题目
17.将函数$f(x)=3sin(2x+\frac{π}{3})$的图象向左平移$\frac{π}{6}$个单位,在向上平移1个单位,得到g(x)的图象,若g(x1)g(2)=16,且${x_1},{x_2}∈[-\frac{3π}{2},\frac{3π}{2}]$,则2x1-x2的最大值为( )
| A. | $\frac{23}{12}π$ | B. | $\frac{35}{12}π$ | C. | $\frac{19}{6}π$ | D. | $\frac{59}{12}π$ |
20.在四面体ABCD中,若AB=CD=$\sqrt{3}$,AC=BD=2,AD=BC=$\sqrt{5}$,则直线AB与CD所成角的余弦值为( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
17.在(1-2x)7(1+x)的展开式中,含x2项的系数为( )
| A. | 71 | B. | 70 | C. | 21 | D. | 49 |
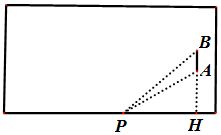 如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.
如图所示的矩形是长为100码,宽为80码的足球比赛场地.其中PH是足球场地边线所在的直线,AB是球门,且AB=8码.从理论研究及经验表明:当足球运动员带球沿着边线奔跑时,当运动员(运动员看做点P)所对AB的张角越大时,踢球进球的可能性就越大.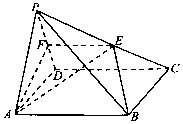 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.