题目内容
20.在四面体ABCD中,若AB=CD=$\sqrt{3}$,AC=BD=2,AD=BC=$\sqrt{5}$,则直线AB与CD所成角的余弦值为( )| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
分析 如图所示,构造长方体,求出长方体的长、宽、高,EF∥AB,∠FOC为直线AB与CD所成角,利用余弦定理可得结论.
解答 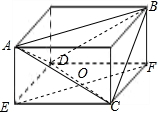 解:如图所示,构造长方体,设长方体的长、宽、高分别为a,b,c,则
解:如图所示,构造长方体,设长方体的长、宽、高分别为a,b,c,则
$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=3}\\{{b}^{2}+{c}^{2}=4}\\{{a}^{2}+{c}^{2}=5}\end{array}\right.$,∴a=$\sqrt{2}$,b=1,c=$\sqrt{3}$,
即CE=1,CF=$\sqrt{2}$,FB=$\sqrt{3}$,
∵EF∥AB,
∴∠FOC为直线AB与CD所成角,
△OCF中,OC=OF=$\frac{\sqrt{3}}{2}$,CF=$\sqrt{2}$,∴cos∠FOC=$\frac{\frac{3}{4}+\frac{3}{4}-2}{2×\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}}$=$\frac{1}{3}$,
故选D.
点评 本题考查异面直线所成角,考查余弦定理的运用,正确构造长方体是关键.

练习册系列答案
相关题目
11. 如图是一个算法的流程图,则输出K值是( )
如图是一个算法的流程图,则输出K值是( )
 如图是一个算法的流程图,则输出K值是( )
如图是一个算法的流程图,则输出K值是( )| A. | 6 | B. | 7 | C. | 16 | D. | 19 |
12.函数$f(x)=\left\{\begin{array}{l}{log_3}(3-x),x≤0\\ f(x-1),x>0\end{array}\right.$,则f(3)的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
8.函数y=cos2x-sin2x+2sinxcosx的值域是( )
| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [$-\sqrt{2}$,$\sqrt{2}$] | D. | [-2,2] |
5.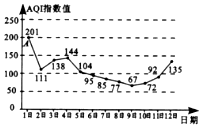 AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
 AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )| A. | 这12天中有6天空气质量为“优良” | B. | 这12天中空气质量最好的是4月9日 | ||
| C. | 这12天的AQI指数值的中位数是90 | D. | 从4日到9日,空气质量越来越好 |
9.若复数z=(x2+2x-3)+(x+3)i为纯虚数,则实数x的值为( )
| A. | -3 | B. | 1 | C. | -3或1 | D. | -1或3 |
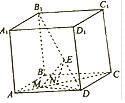 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1.