题目内容
2.某市公租房的房源位于A,B,C,D四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:(1)求所有的申请情况总数;
(2)求甲、乙两位申请同一片区房源的概率.
分析 (1)通过列举法求出答案即可;
(2)列举出甲、乙两位申请人申请同一片区房源的所有情况,从而求出满足条件的概率即可.
解答 解:(1)甲、乙两位申请情况有:
(A,A),(A,B),(A,C),(A,D),(B,A),
(B,B),(B,C),(B,D),(C,A),(C,B),
(C,C),(C,D),(D,A),(D,B),(D,C),
(D,D).共16种结果.
(2)甲、乙两位申请人申请同一片区房源有:
(A,A),(B,B),(C,C),(D,D)共4种结果.
∴所以甲、乙两位申请人申请同一片区房源的概率为$p=\frac{4}{16}=\frac{1}{4}$.
点评 本题考查概率的求法,是一道基础题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
12.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤0}\\{-lnx,x>0}\end{array}\right.$若关于x的方程f2(x)+f(x)+m=0有三个不同实数根,则m的取值范围是( )
| A. | $m<\frac{1}{4}$ | B. | m≤-2 | C. | $-2≤m<\frac{1}{4}$ | D. | m>2 |
17.已知b∈R,i是虚数单位,若2-i与2+bi互为共轭复数,则(2-bi)2=( )
| A. | 3+4i | B. | 3-4i | C. | 5-4i | D. | 5+4i |
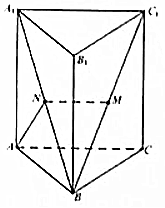 如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.
如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.