��Ŀ����
12����֪��A��B������ֱ�Ϊ��2��0������-2��0����ֱ��AT��BT�����T�������ǵ�б��֮��Ϊ����-�ˣ��ˣ�0���ˡ�1������T�Ĺ켣�Լ�A��B���㹹������C����������C�ķ��̣������佹�����ꣻ
������0���ˣ�1��������C�ϵĵ㵽�佹����������Ϊ1����ֱ��l��y=��x-1��������C��E��F���㣬��x���ڵ�Q��ֱ��AE��AF�ֱ�ֱ��x=3�ڵ�N��M�����߶�MN���е�ΪP��ֱ��PQ��б��Ϊk�䣮��֤��k•k��Ϊ��ֵ��
���� ��1����T��x��y��������ֱ�ߵ�б�ʹ�ʽ��ȡ��б��֮��������������$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{4��}=1$���ˣ�0���ˡ�1�����ݦ˵�ȡֵ��Χ�������Բ���̼��������ꣻ
��2����Բ����˵㵽ͬ�ཹ��ľ�������Բ�ϵĵ㵽�����������룬��æ˵�ֵ�������������C�ķ���Ϊ��ֱ��y=k��x-1����x����Q��1��0����������Բ���̣��ɴ�����Τ�ﶨ����ֱ�߷��̣������֪������֤��k•k��Ϊ��ֵ��
��� �⣺������T��x��y������$\frac{y}{x+2}$•$\frac{y}{x-2}$=-�ˣ������$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{4{��}^{2}}=1$��x�١�2����
��A��B�����꣨2��0������-2��0����Ҳ������ʽ��
������C��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{4��}=1$���ˣ�0���ˡ�1����
��0���ˣ�1ʱ������C�ǽ�����x���ϵ���Բ������Ϊ��-$\sqrt{1-��}$��0������$\sqrt{1-��}$��0����
���ˣ�1ʱ������C�ǽ�����y���ϵ���Բ������Ϊ��0��-2$\sqrt{��-1}$������0��2$\sqrt{��-1}$����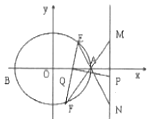
����֤��������0���ˣ�1������C�ǽ�����x���ϵ���Բ���佹��Ϊ��-$\sqrt{1-��}$��0������$\sqrt{1-��}$��0����
��Բ�ij���˵㵽ͬ�ཹ��ľ�������Բ�ϵĵ㵽�����������룮
��2-2$\sqrt{1-��}$=1������=$\frac{3}{4}$��
����C�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
ֱ��y=k��x-1����x����Q��1��0������E��x1��y1����F��x2��y2����
$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$����ȥy�������ã���4k2+3��x2-8k2x+4k2-12=0��
��x1+x2=$\frac{8{k}^{2}}{4{k}^{2}+3}$����x1x2=$\frac{4{k}^{2}-12}{4{k}^{2}+3}$����
ֱ��AE����Ϊ��y=$\frac{{y}_{1}}{{x}_{1}-2}$��x-2������ֱ��x=3�ڵ�N��3��$\frac{{y}_{1}}{{x}_{1}-2}$����
ֱ��AF����Ϊ��y=$\frac{{y}_{2}}{{x}_{2}-2}$��x-2������ֱ��x=3�ڵ㣨3��$\frac{{y}_{2}}{{x}_{2}-2}$����
���߶�MN���е�ΪP��3��$\frac{1}{2}$��$\frac{{y}_{1}}{{x}_{1}-2}$+$\frac{{y}_{2}}{{x}_{2}-2}$������
��ֱ��PQ��б��Ϊ��
k��=$\frac{\frac{1}{2}��\frac{{y}_{1}}{{x}_{1}-2}+\frac{{y}_{2}}{{x}_{2}-2}��}{3-1}$=$\frac{{y}_{1}{x}_{2}+{y}_{2}{x}_{1}-2��{y}_{1}+{y}_{2}��}{4[{x}_{1}{x}_{2}-2��{x}_{1}+{x}_{2}��+4]}$=$\frac{2k{x}_{1}{x}_{2}-3k��{x}_{1}+{x}_{2}��+4k}{4[{x}_{1}{x}_{2}-2��{x}_{1}+{x}_{2}��+4]}$��
���٢ڴ����ʽ�����k��=-$\frac{3}{4k}$��
��k•k��=-$\frac{3}{4}$��
��k•k��Ϊ��ֵ��
���� ���⿼�����߷��̼������������������ֱ�ߵ�б��֮��Ϊ��ֵ��֤�������е��⣬����ʱҪ�������⣬ע����Բ���ʡ�Τ�ﶨ����ֱ�߷��̵����ʵĺ������ã������е��⣮

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�| A�� | $x=-\frac{��}{3}$ | B�� | $x=\frac{��}{3}$ | C�� | $x=\frac{��}{6}$ | D�� | $x=\frac{2��}{3}$ |
| A�� | a��b��0 | B�� | b��a | C�� | a��b��0 | D�� | ab��a-b����0 |
| A�� | $\frac{21}{25}$ | B�� | $\frac{25}{21}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{5}{4}$ |
 ��ͼ����֪����ABCD�ı߳�Ϊ6����BAD=60�㣬AC��BD=0��������ABCD�ضԽ���AC���𣬵õ�����B-ACD����M����BC���е㣮
��ͼ����֪����ABCD�ı߳�Ϊ6����BAD=60�㣬AC��BD=0��������ABCD�ضԽ���AC���𣬵õ�����B-ACD����M����BC���е㣮