题目内容
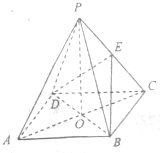 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:(1)PA∥平面BDE;
(2)BD⊥平面PAC;
(3)若PA=AB=2,求二面角E-BD-C的大小.
考点:二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)连接OE,由已知得OE∥AP,由此能证明PA∥平面BDE.
(2)由线面垂直得PO⊥BD,由正方形性质得BD⊥AC,由此能证明BD⊥平面PAC.
(3)以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,求出平面BDE的法向量和平面BDC的法向量,由此能求出二面角E-BD-C的大小.
(2)由线面垂直得PO⊥BD,由正方形性质得BD⊥AC,由此能证明BD⊥平面PAC.
(3)以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,求出平面BDE的法向量和平面BDC的法向量,由此能求出二面角E-BD-C的大小.
解答:
(1)证明:如图所示,连接OE,
∵O是正方形ABCD的中心,∴OC=OA,
∵E是PC的中点,∴CE=EP,
∴OE∥AP,
∵PA?平面BDE,OE?平面BDE,
∴PA∥平面BDE.
(2)证明:∵PO⊥底面ABCD,∴PO⊥BD.
由正方形可得:BD⊥AC,
又PO∩AC=O,∴BD⊥平面PAC.
(3)解:以O为原点,OA为x轴,OB为y轴,OP为z轴,
建立空间直角坐标系,
∵PA=AB=2,∴B(0,
,0),D(0,-
,0),
C(-
,0,0),P(0,0,
),E(-
,0,
),
=(0,2
,0),
=(-
,-
,
),
设平面BDE的法向量
=(x,y,z),
则
,
取y=1,得
=(0,1,2),
又平面BDC的法向量
=(0,0,1),
设二面角E-BD-C的平面角为θ,
cosθ=|
|=
=
.
∴二面角E-BD-C的大小为arccos
.

∵O是正方形ABCD的中心,∴OC=OA,
∵E是PC的中点,∴CE=EP,
∴OE∥AP,
∵PA?平面BDE,OE?平面BDE,
∴PA∥平面BDE.
(2)证明:∵PO⊥底面ABCD,∴PO⊥BD.
由正方形可得:BD⊥AC,
又PO∩AC=O,∴BD⊥平面PAC.
(3)解:以O为原点,OA为x轴,OB为y轴,OP为z轴,
建立空间直角坐标系,
∵PA=AB=2,∴B(0,
| 2 |
| 2 |
C(-
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| BD |
| 2 |
| BE |
| ||
| 2 |
| 2 |
| ||
| 2 |
设平面BDE的法向量
| n |
则
|
取y=1,得
| n |
又平面BDC的法向量
| m |
设二面角E-BD-C的平面角为θ,
cosθ=|
| ||||
|
|
| 1 | ||
|
| ||
| 5 |
∴二面角E-BD-C的大小为arccos
| ||
| 5 |
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,线面直行、线面垂直、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于( )
高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于( )| A、112 | B、114 |
| C、116 | D、120 |
下列函数f(x)中,满足“对任意x1,x2∈(-∞,0),当x1<x2时,都有f(x1)<f(x2)”的函数是( )
| A、f(x)=-x+1 |
| B、f(x)=x2-1 |
| C、f(x)=2x |
| D、f(x)=ln(-x) |
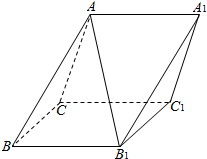 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.