题目内容
7.已知函数f(x)=3x,g(x)=|x+a|-3,其中a∈R.(Ⅰ)若函数h(x)=f[g(x)]的图象关于直线x=2对称,求a的值;
(Ⅱ)给出函数y=g[f(x)]的零点个数,并说明理由.
分析 (Ⅰ)函数h(x)=f[g(x)]=3|x+a|-3 的图象关于直线x=2对称,则h(4-x)=h(x)⇒|x+a|=|4-x+a|恒成立⇒a=-2;
(Ⅱ)函数y=g[f(x)]=|3x+a|-3的零点个数,就是函数G(x)=|3x+a|与y=3的交点,
分①当0≤a<3时;②当a≥3时;③-3≤a<0时;④当a<-3时,画出图象判断个数.
解答 解:(Ⅰ)函数h(x)=f[g(x)]=3|x+a|-3 的图象关于直线x=2对称,则h(4-x)=h(x)⇒|x+a|=|4-x+a|恒成立⇒a=-2;
(Ⅱ)函数y=g[f(x)]=|3x+a|-3的零点个数,就是函数G(x)=|3x+a|与y=3的交点,
①当0≤a<3时,G(x)=|3x+a|=3x+a与y=3的交点只有一个,即函数y=g[f(x)]的零点个数为1个(如图1);
②当a≥3时,G(x)=|3x+a|=3x+a与y=3没有交点,即函数y=g[f(x)]的零点个数为0个(如图1);
③-3≤a<0时,G(x)=|3x+a|与y=3的交点只有1个(如图2);
④当a<-3时,G(x)=|3x+a|与y=3的交点有2个(如图2);

点评 本题考查了函数的零点,把零点个数转化为两函数交点个数是常用方法,属于中档题.

练习册系列答案
相关题目
17.若一抛物线的顶点在原点,焦点为F(0,$\frac{1}{2}$),在该抛物线的方程为( )
| A. | y2=$\frac{1}{8}$x | B. | y2=2x | C. | y=2x2 | D. | y=$\frac{1}{2}$x2 |
18.若a=2log32,b=log${\;}_{\frac{1}{4}}$2,$c={2^{-\frac{1}{3}}}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
15.下列各式正确的是( )
| A. | (cosx)′=sinx | B. | (ax)′=axlna | C. | ${({sin\frac{π}{12}})^'}=cos\frac{π}{12}$ | D. | ${({{x^{-5}}})^'}=-\frac{1}{5}{x^{-6}}$ |
8.若α为第四象限角,则$\sqrt{\frac{1+cosα}{1-cosα}}+\sqrt{\frac{1-cosα}{1+cosα}}$=( )
| A. | $-\frac{2}{sinα}$ | B. | $-\frac{2}{tanα}$ | C. | $\frac{2}{{co{s}α}}$ | D. | $-\frac{2}{sinαcosα}$ |
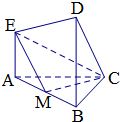 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M是AB的中点.