题目内容
已知
=（2，2
-4），
=（1，1），求
与
的夹角为 ．
| a |
| 3 |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的数量积的坐标表示和向量的模的公式，以及向量夹角的公式，计算即可得到所求值．
解答：
解：由
=（2，2
-4），
=（1，1），
则|
|=
=4
，|
|=
．
•
=2+2
-4=2（
-1）．
则有cos＜
，
＞=
=
=
=
，
由于0≤＜
，
＞≤π，
则有
与
的夹角为
．
故答案为：
．
| a |
| 3 |
| b |
则|
| a |
4+(2
|
2-
|
| b |
| 2 |
| a |
| b |
| 3 |
| 3 |
则有cos＜
| a |
| b |
| ||||
|
|
2(
| ||||||
4
|
| ||||||
2
|
| 1 |
| 2 |
由于0≤＜
| a |
| b |
则有
| a |
| b |
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查平面向量的数量积的坐标表示和向量的模的公式，考查向量的夹角的求法，考查运算能力，属于基础题．
练习册系列答案
相关题目
下列各组数据中，数值相等的是（ ）
| A、（25）10和（10110）2 |
| B、（13）10和（1101）2 |
| C、（11）10和（1100）2 |
| D、（10）10和（10）2 |
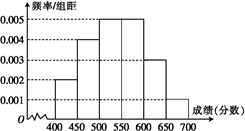为对考生的月考成绩进行分析，某地区随机抽查了10000名考生的成绩，根据所得数据画了如下的样本频率分布直方图．