题目内容
19.一条渐近线方程为$y=\frac{1}{2}x$且过点(4,1)的双曲线的方程为$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1.分析 由渐近线方程为$y=\frac{1}{2}x$,可设双曲线的方程为y2-$\frac{1}{4}$x2=λ(λ≠0),代入点(4,1),解方程即可得到所求双曲线的方程.
解答 解:由一条渐近线方程为$y=\frac{1}{2}x$,
可设双曲线的方程为y2-$\frac{1}{4}$x2=λ(λ≠0),
代入点(4,1),可得λ=1-$\frac{1}{4}$×16=-3,
即有双曲线的方程为y2-$\frac{1}{4}$x2=-3,
即为$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1.
故答案为:$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1.
点评 本题考查双曲线的方程的求法,注意运用双曲线的渐近线方程和双曲线的方程的关系,考查运算能力,属于基础题.

练习册系列答案
相关题目
10.双曲线$\frac{y^2}{12}-\frac{x^2}{4}=1$的焦点到渐近线的距离为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
7.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺3$\frac{1}{3}$寸,容纳米2000斛(1丈=10尺,l尺=10寸,斛为容积单位,l斛≈1.62立方尺,π≈3),则圆柱底圆周长约为( )
| A. | l丈3尺 | B. | 5丈4尺 | C. | 9丈2尺 | D. | 48丈6尺 |
9.在空间中,已知$\overrightarrow{AB}$=(2,4,0),$\overrightarrow{BC}$=(-1,3,0),则∠ABC的大小为( )
| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知:∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC,直线SD与平面ABCD所成角的正弦值为$\frac{\sqrt{11}}{11}$.O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知:∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC,直线SD与平面ABCD所成角的正弦值为$\frac{\sqrt{11}}{11}$.O为BC的中点.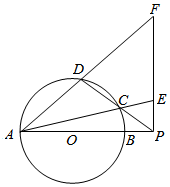 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.