题目内容
11.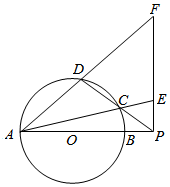 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.(Ⅰ) 当∠PEC=60°时,求∠PDF的度数;
(Ⅱ) 求PE•PF的值.
分析 (Ⅰ)连结BC,依题意知,∠CAB+∠CBA=∠EAP+∠PEC,继而可得∠CBA=∠PEC,又∠PEC=60°,于是可得∠PDF=∠CBA=∠PEC=60°;
(Ⅱ) 解法1:由(Ⅰ)知∠PDF=∠PEC,利用D、C、E、F四点共圆PE•PF=PC•PD,及割线定理可得PC•PD=PB•PA=24,于是可得答案;
解法2:由∠PEC=∠PDF,∠EPC=∠DPF可得△PEC~△PDF,从而可得PE•PF=PC•PD,再结合PC、PA都是圆O的割线,得到PC•PD=PB•PA=24,从而可求得PE•PF的值.
解答 解:(Ⅰ) 连结BC,∵AB是圆O的直径,∴则∠ACB=90°,-----(1分)
又∠APF=90°,∠CAB+∠CBA=∠EAP+∠PEC--------------(2分)
∴∠CBA=∠PEC,--------------------------------------(3分)
∵∠PEC=60°∴∠PDF=∠CBA=∠PEC=60°;-------------(4分)
(Ⅱ) 解法1:由(Ⅰ)知∠PDF=∠PEC,
∴D、C、E、F四点共圆,---------------------------------(6分)
∴PE•PF=PC•PD,-----------------------------------------------------------(7分)
∵PC、PA都是圆O的割线,∴PC•PD=PB•PA=24,------------------------------(9分)
∴PE•PF=24.----------------------------------------------------------------(10分)
解法2:∵∠PEC=∠PDF,∠EPC=∠DPF,-----------------------------------(6分)
∴△PEC~△PDF-------------------------------------------------------------(7分)
∴$\frac{PE}{PD}=\frac{PC}{PF}$即PE•PF=PC•PD,-----------------------------------------------(8分)
∵PC、PA都是圆O的割线,∴PC•PD=PB•PA=24--------------------------------(9分)
∴PE•PF=24.---------------------------------------------------------------(10分)
点评 本题考查与圆有关的线段的求法,考查相似三角形与割线定理的应用,解题时要认真审题,注意圆的简单性质、三角形相似的性质的合理运用,属于中档题.

 口算能手系列答案
口算能手系列答案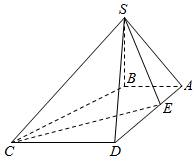 如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )
如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | sin1°<sin1<sinπ° | B. | sin1°<sinπ°<sin1 | ||
| C. | sinπ°<sin1°<sin1 | D. | sin1<sin1°<sinπ° |
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
 已知长方形ABCD中,AB=3,AD=4,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
已知长方形ABCD中,AB=3,AD=4,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.