题目内容
4.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{2}=1(a>0)$与抛物线y2=8x的焦点重合,直线y=x+1与该双曲线的交点个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
分析 求得抛物线的焦点,可得c=2,由a,b,c的关系可得a,进而得到双曲线的方程,联立直线y=x+1,解方程可得交点个数.
解答 解:抛物线y2=8x的焦点为(2,0),
由题意可得c=2,即a2+b2=4,
即a2+2=4,解得a=$\sqrt{2}$,
可得双曲线的方程为x2-y2=2,
将直线y=x+1代入双曲线的方程,可得
x2-(x+1)2=2,解得x=-$\frac{3}{2}$,
故直线y=x+1与该双曲线的交点个数为1.
故选:B.
点评 本题考查双曲线的方程和运用,注意联立直线方程,求交点,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.sin1°,sin1,sinπ°的大小顺序是( )
| A. | sin1°<sin1<sinπ° | B. | sin1°<sinπ°<sin1 | ||
| C. | sinπ°<sin1°<sin1 | D. | sin1<sin1°<sinπ° |
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.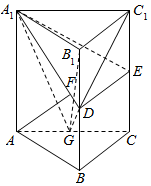 如图,在直三棱柱ABC-A1B1C1中,D,E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.
如图,在直三棱柱ABC-A1B1C1中,D,E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.