题目内容
以下命题:
①△ABC中,若a,b,c成等比,则∠B∈(0,
];
②数列{an}的前n项为Sn,若an+1=2Sn(n∈N*),则{an}为等比数列;
③一个几何体的主视图和左视图为全等的两个等腰Rt△,则其俯视图一定不能为等边三角形;
④腰长为1的等腰Rt△绕其斜边旋转一周所得的几何体的表面积为(
+
)π.
其中正确的命题为 .
①△ABC中,若a,b,c成等比,则∠B∈(0,
| π |
| 3 |
②数列{an}的前n项为Sn,若an+1=2Sn(n∈N*),则{an}为等比数列;
③一个几何体的主视图和左视图为全等的两个等腰Rt△,则其俯视图一定不能为等边三角形;
④腰长为1的等腰Rt△绕其斜边旋转一周所得的几何体的表面积为(
| 2 |
| 1 |
| 2 |
其中正确的命题为
考点:命题的真假判断与应用
专题:等差数列与等比数列,解三角形,空间位置关系与距离
分析:①由等比数列的性质和余弦定理,基本不等式即可求出B的范围;
②由数列的通项和求和之间的关系,即可判断,注意n从2开始;
③画出三棱锥,若其俯视图为等边三角形,推出左视图与主视图不全等,即可判断;
④画出腰长为1的等腰Rt△绕其斜边旋转一周所得的几何体如图,两个圆锥倒扣在一起,求出表面积.
②由数列的通项和求和之间的关系,即可判断,注意n从2开始;
③画出三棱锥,若其俯视图为等边三角形,推出左视图与主视图不全等,即可判断;
④画出腰长为1的等腰Rt△绕其斜边旋转一周所得的几何体如图,两个圆锥倒扣在一起,求出表面积.
解答:
 解:①△ABC中,若a,b,c成等比,则b2=ac,由cosB=
解:①△ABC中,若a,b,c成等比,则b2=ac,由cosB=
=
=
-
≥
-
=
,由B为三角形的内角,
得0<B≤
,故①对;
②数列{an}的前n项为Sn,若an+1=2Sn(n∈N*),则a2=2S1=2a1,
将n换为n-1,得,an=2Sn-1,有an+1-an=2an,即an+1=3an(n=2,3,…),
故②错;
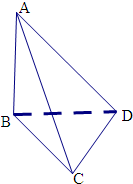
③一个几何体的主视图和左视图为全等的两个等腰Rt△,
若其俯视图为等边三角形,如图,AB⊥平面BCD,且△BCD是等边△,
则左视图与主视图不全等,矛盾,故③对;
④腰长为1的等腰Rt△绕其斜边旋转一周所得的几何体如图,
两个圆锥倒扣在一起,高为
,底面半径为
,
则表面积为2×π×
×1=
π,故④错.
故答案为:①③
 解:①△ABC中,若a,b,c成等比,则b2=ac,由cosB=
解:①△ABC中,若a,b,c成等比,则b2=ac,由cosB=| a2+c2-b2 |
| 2ac |
| a2+c2-ac |
| 2ac |
| a2+c2 |
| 2ac |
| 1 |
| 2 |
| 2ac |
| 2ac |
| 1 |
| 2 |
| 1 |
| 2 |
得0<B≤
| π |
| 3 |
②数列{an}的前n项为Sn,若an+1=2Sn(n∈N*),则a2=2S1=2a1,
将n换为n-1,得,an=2Sn-1,有an+1-an=2an,即an+1=3an(n=2,3,…),
故②错;
③一个几何体的主视图和左视图为全等的两个等腰Rt△,
若其俯视图为等边三角形,如图,AB⊥平面BCD,且△BCD是等边△,

则左视图与主视图不全等,矛盾,故③对;
④腰长为1的等腰Rt△绕其斜边旋转一周所得的几何体如图,
两个圆锥倒扣在一起,高为
| ||
| 2 |
| ||
| 2 |
则表面积为2×π×
| ||
| 2 |
| 2 |
故答案为:①③
点评:本题考查解直角三角形的余弦定理和基本不等式的运用,考查数列的通项和求和之间的关系,考查空间几何体的三视图和旋转体的表面积,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
圆p:x2+y2=5,则经过点M(-1,2)的切线方程为( )
| A、x-2y-5=0 |
| B、x+2y+5=0 |
| C、x+2y-5=0 |
| D、x-2y+5=0 |