题目内容
5.周期函数f(x)的定义域为R,周期为2,且当-1<x≤1时,f(x)=1-x2.若直线y=-x+a与曲线y=f(x)恰有3个交点,则实数a的取值范围是( )| A. | 2k+$\frac{3}{4}$<a<2k+$\frac{5}{4}$,k∈Z | B. | 2k+1<a<2k+3,k∈Z | ||
| C. | 2k+1<a<2k+$\frac{5}{4}$,k∈Z | D. | 2k-$\frac{3}{4}$<a<2k+1,k∈Z |
分析 由题意画出函数f(x)的图象,并在图中画出关键直线,再由条件转化为求出相切时的切点坐标,利用导数的几何意义,然后再把坐标代入切线方程求出a的值,
解答 解:由题意画出函数f(x)的图象,如下图:
其中图中的直线l的方程为:y=-x+1,此时恰有两个交点,
由图得,当-1<x≤1时,直线l向上平移过程中与曲线y=f(x)恰有3个交点,
直到相切时,
设切点为p(x,y),则f′(x)=-2x,
∴-1=-2x,解得x=$\frac{1}{2}$,即y=f($\frac{1}{2}$)=1-$\frac{1}{4}$=$\frac{3}{4}$,
∴p($\frac{1}{2}$,$\frac{3}{4}$),代入切线y=-x+a,解得a=$\frac{5}{4}$,
∵f(x)的定义域为R,周期为2,
∴所求的a的集合是:2k+1<a<2k+$\frac{5}{4}$,k∈Z,
故选C.
点评 本题考查了函数的性质以及图象的应用,导数的几何意义,考查了数形结合思想,关键正确作图.

练习册系列答案
相关题目
14.已知$\overrightarrow{a}$、$\overrightarrow{b}$均为单位向量,(2$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=-$\frac{3\sqrt{3}}{2}$,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
15.若b<a<0,则下列不等式一定成立的是( )
| A. | a3<b3 | B. | ab>b2 | C. | ac2>bc2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
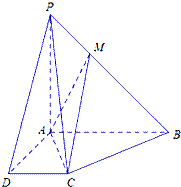 如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.