题目内容
14.已知$\overrightarrow{a}$、$\overrightarrow{b}$均为单位向量,(2$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=-$\frac{3\sqrt{3}}{2}$,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 推导出(2$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=-3cos<$\overrightarrow{a},\overrightarrow{b}$>=-$\frac{3\sqrt{3}}{2}$,由此能求出向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角.
解答 解:∵$\overrightarrow{a}$、$\overrightarrow{b}$均为单位向量,(2$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=-$\frac{3\sqrt{3}}{2}$,
∴(2$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=$2{\overrightarrow{a}}^{2}-3\overrightarrow{a}•\overrightarrow{b}-2{\overrightarrow{b}}^{2}$
=-3×$1×1×cos<\overrightarrow{a},\overrightarrow{b}>$=-3cos<$\overrightarrow{a},\overrightarrow{b}$>=-$\frac{3\sqrt{3}}{2}$,
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\sqrt{3}}{2}$.
∴<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{π}{6}$.
∴向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{6}$.
故选:D.
点评 本题考查向量的夹角的求法,是中档题,解题时要认真审题,注意向量数量积公式的合理运用.

| A. | 2k+$\frac{3}{4}$<a<2k+$\frac{5}{4}$,k∈Z | B. | 2k+1<a<2k+3,k∈Z | ||
| C. | 2k+1<a<2k+$\frac{5}{4}$,k∈Z | D. | 2k-$\frac{3}{4}$<a<2k+1,k∈Z |
 如图是一几何体的直观图、主视图和俯视图,则该几何体的侧视图是( )
如图是一几何体的直观图、主视图和俯视图,则该几何体的侧视图是( )



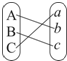 连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;
连线方式表示为$(\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array})$,规定第一行A,B,C的顺序固定不变,请列出所有连线的情况;