函数f}{x-2}$.x∈[1.5.3]的值域为(0.3ln2]．题目和参考答案——青夏教育精英家教网—

题目内容

13．函数f（x）=$\frac{xln（x-1）}{x-2}$，x∈[1.5，3]的值域为（0，3ln2]．

分析利用导函数研究函数f（x）的单调性，利用单调性求其值域．

解答解：函数f（x）=$\frac{xln（x-1）}{x-2}$，x∈[1.5，3]，且x≠2．
则f′（x）=$\frac{[xln（x-1）]′（x-2）-（x-2）′[xln（x-1）]}{（x-2）^{2}}$，
令f′（x）=0，
解得：x=2．
∵x∈[1.5，3]，且x≠2．
当1.5≤x＜2，f′（x）＜0，故而f（x）是单调递减，且f（x）＞0．
当2＜x≤3，f′（x）＞0，故而f（x）是单调递增，且f（x）＞0．
∴f（x）＞0．
当x=3时，取得最大值为3ln2．
得函数f（x）的值域为（0，3ln2]．
故答案为：（0，3ln2]．

点评本题考查了函数值域的求法．高中函数值域求法有：1、观察法，2、配方法，3、反函数法，4、判别式法；5、换元法，6、数形结合法，7、不等式法，8、分离常数法，9、单调性法，10、利用导数求函数的值域，11、最值法，12、构造法，13、比例法．要根据题意选择．

练习册系列答案

8．设y=f（x）在区间[0，1]上是非负连续函数．
试证：存在x₀∈（0，1），使得在区间[0，x₀]上以f（x₀）为高的矩形面积等于在区间[x₀，1]上以y=f（x）为曲边的曲边梯形的面积．

8．复数z₁，z₂满足|z₁|=|z₂|=1，|z₁+z₂|=$\sqrt{2}$，则|z₁-z₂|=（　　）

18．在数列{a_n}中，a₁=2，2（a_n+1-1）（a_n-1）+a_n+1-a_n=0（n∈N^*），若a_n＜$\frac{201}{199}$，则n的最小值为（　　）

5．周期函数f（x）的定义域为R，周期为2，且当-1＜x≤1时，f（x）=1-x²．若直线y=-x+a与曲线y=f（x）恰有3个交点，则实数a的取值范围是（　　）

	A．	2k+$\frac{3}{4}$＜a＜2k+$\frac{5}{4}$，k∈Z		B．	2k+1＜a＜2k+3，k∈Z
	C．	2k+1＜a＜2k+$\frac{5}{4}$，k∈Z		D．	2k-$\frac{3}{4}$＜a＜2k+1，k∈Z

2．某超市有奖促销，抽奖规则是：每消费满50元，即可抽奖一次．抽奖方法是：在不透明的盒内装有标着1，2，3，4，5号码的5个小球，从中任取1球，若号码大于3就奖励10元，否则无奖，之后将球放回盒中，即完成一次抽奖，则某人抽奖2次恰中20元的概率为$\frac{4}{25}$；若某人消费200元，则他中奖金额的期望是16元．

3．某学校为了增强学生对消防安全知识的了解，举行了一次消防安全知识竞赛．其中一道题是连线题，要求将3种不同的消防工具与它们的用途一对一连线，规定：每连对一条得2分，连错一条扣1分，参赛者必须把消防工具与用途一对一全部连起来．
（Ⅰ）设三种消防工具分别为A，B，C，其用途分别为a，b，c，若把

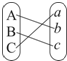连线方式表示为$（\begin{array}{l}{A^{\;}}{B^{\;}}C\\{b^{\;}}{c^{\;}}a\end{array}）$，规定第一行A，B，C的顺序固定不变，请列出所有连线的情况；
（Ⅱ）求某参赛者得分为0分的概率．

试题分类