题目内容
 函数f(x)=2sin(
函数f(x)=2sin(| π |
| 4 |
A、-
| ||
B、
| ||
| C、1 | ||
| D、0 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
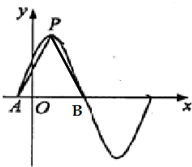
分析:由题意根据函数的周期,推出AB的长度,得到P到AB的距离,即可求出tan∠PAB.
解答:
解:∵P是f(x)=2sin(
x+φ)图象的最高点,A,B是图象与x轴的交点,
∴AB=
•
=4,P到AB的距离为2,
∴tan∠PAB=
=1.
故选:C
| π |
| 4 |
∴AB=
| 1 |
| 2 |
| 2π | ||
|
∴tan∠PAB=
| 2 | ||
|
故选:C
点评:本题考查三角函数的图象的应用,涉及三角形的解法,属基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
在极坐标系中,过点(2,
)且与极轴平行的直线方程是( )
| π |
| 2 |
| A、ρ=2 | ||
B、θ=
| ||
| C、ρcosθ=2 | ||
| D、ρsinθ=2 |
中国古代数学著作《九章算法》中的“更相减损术”可用来求两个正整数的最大公约数.现应用此法求168与93的最大公约数:记(168,93)为初始状态,则第一步可得(75,93),第二步得到(75,18),第三步得到(57,18),第四步将得到( )
| A、(57,18) |
| B、(39,3) |
| C、(39,18) |
| D、(21,18) |
若实数x,y满足不等式组
,则y-x的最大值为( )
|
| A、1 | B、0 | C、-1 | D、-3 |