题目内容
已知函数f(x)=
,g(x)=|x-k|+|x-1|,若对任意的x1,x2∈R,都有f(x1)≤g(x2)成立,则实数k的取值范围为 .
|
考点:分段函数的应用
专题:综合题,函数的性质及应用
分析:求出函数f(x)=
的最大值为
,g(x)=|x-k|+|x-1|的最小值为|1-k|,可得
≤|1-k|,即可求出实数k的取值范围.
|
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:由题意函数f(x)=
的最大值为
,g(x)=|x-k|+|x-1|的最小值为|1-k|,
∵对任意的x1,x2∈R,都有f(x1)≤g(x2)成立,
∴
≤|1-k|,
∴k≤
或k≥
.
故答案为:k≤
或k≥
.
|
| 1 |
| 4 |
∵对任意的x1,x2∈R,都有f(x1)≤g(x2)成立,
∴
| 1 |
| 4 |
∴k≤
| 3 |
| 4 |
| 5 |
| 4 |
故答案为:k≤
| 3 |
| 4 |
| 5 |
| 4 |
点评:本题考查分段函数的应用,考查函数的最值,确定函数的最值是关键.

练习册系列答案
相关题目
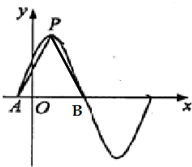 函数f(x)=2sin(
函数f(x)=2sin(| π |
| 4 |
A、-
| ||
B、
| ||
| C、1 | ||
| D、0 |
请仔细观察,运用合情推理,写在下面括号里的数最可能的是1,1,2,3,5,( ),13.
| A、8 | B、9 | C、10 | D、11 |