题目内容
设a为非零常数，已知（x2+
）(x-
)6的展开式中各项系数和为2，则展开式中常数项等于 ．
| 1 |
| x |
| a |
| x |
考点：二项式系数的性质
专题：计算题,二项式定理
分析：根据（x2+
）(x-
)6的展开式中各项系数和为2，令x=1得a=2，再利用展开式的通项公式，求出展开式中常数项．
| 1 |
| x |
| a |
| x |
解答：
解：∵（x2+
）(x-
)6的展开式中各项系数和为2，
∴令x=1得a=2或a=0（舍）．
又Tr+1=
(-2)rx6-2r(r=0，1，2，…，6)
6-2r为偶数，故6-2r=-2即r=4．
∴(x2+
)(x-
)6的展开式的常数项为
(-2)4=240．
| 1 |
| x |
| a |
| x |
∴令x=1得a=2或a=0（舍）．
又Tr+1=
| C | r 6 |
6-2r为偶数，故6-2r=-2即r=4．
∴(x2+
| 1 |
| x |
| 2 |
| x |
| C | 4 6 |
点评：本题考查二项展开式的通项公式解决二项展开式的特定项问题；考查求展开式的各项系数和的常用方法是赋值法．
练习册系列答案
相关题目
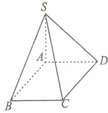如图，在四棱锥S-ABCD中，底面ABCD是菱形，SA⊥平面ABCD
