题目内容
15．在△ABC中，已知角A、B、C所对的边分别为a，b，c．已知A=$\frac{π}{3}$，a=$\sqrt{3}$，b=2．则B=（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
分析 利用正弦定理即可得出．
解答 解：在△ABC中，由正弦定理可得：$\frac{a}{sinA}$=$\frac{b}{sinB}$，
∴sinB=$\frac{bsinA}{a}$=$\frac{2sin\frac{π}{3}}{\sqrt{3}}$=1，
又B∈（0，π），∴B=$\frac{π}{2}$．
故选：D．
点评 本题考查了正弦定理的应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
5．
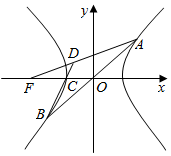如图，双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）左焦点、左顶点分别为F，C，过原点O的直线与两分支分别交于A，B（异于C点），若直线AF交BC于D点，且$\overrightarrow{AD}$=2$\overrightarrow{DF}$，则双曲线的离心率为（ ）
如图，双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）左焦点、左顶点分别为F，C，过原点O的直线与两分支分别交于A，B（异于C点），若直线AF交BC于D点，且$\overrightarrow{AD}$=2$\overrightarrow{DF}$，则双曲线的离心率为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | $\frac{3}{2}$ |
3．已知F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，且双曲线C的焦距为2c，定点G（0，c），若双曲线C上存在点P满足|PF|=|PG|，则双曲线的离心率的取值范围是（ ）
| A． | （$\sqrt{2}$，+∞） | B． | （1，$\sqrt{2}$） | C． | [$\sqrt{3}$，+∞） | D． | （1，$\sqrt{3}$） |
20．已知f（x）=$\frac{{2}^{x}-1}{{2}^{x}+1}$，则满足f（a）-f（-a）＜1的a的取值范围是（ ）
| A． | （-∞，3） | B． | （-∞，log23） | C． | （3，+∞） | D． | （log23，+∞） |
