题目内容

372和684的最大公约数是
 
．
考点：辗转相除法
专题：计算题
分析：利用两个数中较大的一个除以较小的数字，得到商是1，余数是312，用37除以312，得到商是1，余数是60，用同样的方法进行下去，直到没有余数，所以两个数字的最大公约数是12．
解答： 解：因为684=372×1+312
372=312×1+60
312=60×5+12
60=12×5
所以372和684的最大公约数为12
故答案为：12．
点评：本题考查的知识点是最大公因数，在求两个正整数的最大公因数时，辗转相除法和更相减损术是常用的方法，要熟练掌握．
练习册系列答案
相关题目
若点（a，9）在函数y=3x的图象上，则tan
a
6
π的值为
 
．
关于函数f（x）=4sin（2x+
π
3
）（x∈R），有如下说法：
①y=f（x）的图象可由y=4sin2x的图象上所有的点向左平移
π
3
个单位而得到；
②y=f（x）的图象可由y=4sin（x+
π
3
）图象上所有点的横坐标伸长到原来的2倍  （纵坐标不变）而得到；
③y=f（x）的图象关于点（-
π
6
，0）对称；
④y=f（x）的图象关于直线x=
π
3
对称
其中，正确的说法是
 
（列出所有你认为正确的说法）
关于函数f（x）=cos2x-2
3
sinxcosx，下列命题：
①若存在x1，x2有x1-x2=π时，f（x1）=f（x2）成立；
②f（x）在区间[-
π
6
，
π
3
]上是单调递增；
③函数f（x）的图象关于点（
π
12
，0）成中心对称图象；
④将函数f（x）的图象向右平移
5π
12
个单位后将与y=2sin2x的图象重合．
其中正确的命题序号
 
（注：把你认为正确的序号都填上）
函数f（x）=sinx+cosx，在各项均为正数的数列{an}中对任意的n∈N*都有f（an+x）=f（an-x）成立，则数列{an}的通项公式可以为（写一个你认为正确的）
 
．
若f（x）=f（2-x），且当x∈（-∞，1）时，（x-1）f′（x）＜0，设a=f（0），b=f（
1
2
），C=f（3），则a，b，c大小关系为
 
．
设全集U=R，A={x|x（x+2）＜0，B={x|x＜-1}，则图中阴影部分表示的集合为（　　）
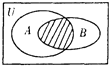
A、{x|-2＜x＜0}
B、{x|-2＜x＜-1}
C、{x|x＞0}
D、{x|x＜-1}
若α，β是两个不同平面，m，n是两条不同直线，则下列命题中不正确的是（　　）
A、α∥β，m⊥α，则m⊥β
B、m∥n，m⊥α，则n⊥α
C、n∥α，n⊥β，则α⊥β
D、α∩β=m，n与α，β所成的角相等，则m⊥n
执行下面的框图，若输入的n是6，则输出p的值是（　　）
A、120B、720
C、1440D、5040

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网