记A=logsin1cos1.B=logsin1tan1.C=logcos1sin1.D=logcos1tan1.则A.B.C.D四个数中最大数与最小值之和为．题目和参考答案——青夏教育精英家教网—

题目内容

记A=log_sin1cos1，B=log_sin1tan1，C=log_cos1sin1，D=log_cos1tan1，则A、B、C、D四个数中最大数与最小值之和为

．

考点：对数值大小的比较,对数的运算性质

专题：函数的性质及应用

分析：利用三角函数的单调性、对数函数的单调性即可得出．

解答： 解：∵tan1＞1＞sin1＞cos1＞0，
∴A=log_sin1cos1=

logcos1sin1

＞log_sin1sin1=1，∴A＞C＞0．
又lgtan1＞0＞lgsin1＞lgcos1，
B=log_sin1tan1=

lgtan1

lgsin1

＜

lgtan1

lgcos1

log_cos1tan1=D＜0，∴0＞D＞B．
综上可得：A＞C＞0＞B＞D．
∴A、B、C、D四个数中最大数与最小值之和为A+B=log_sin1cos1+log_sin1tan1=log_sin1sin1=1，
故答案为：1．

点评：本题考查了三角函数与对数函数的单调性、不等式的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案

相关题目

对应的复数分别为z₁=3+5i，z₂=-1+2i．
（1）求

对应的复数；
（2）求

对的应的复数；
（3）求平行四边形ABCD的面积．

解方程2^x+1-1=4，得x=

．

曲线f（x）=x²•（x-2）+1在点（1，f（1））处的切线方程为

．

已知函数f（x）=x²+bx+c（b，c∈R），g（x）=2x+b，且对于任意x∈R，恒有g（x）≤f（x）．
（1）证明：c≥1，c≥|b|
（2）设函数h（x）满足：f（x）+h（x）=（x+c）²．证明：函数h（x）在（0，+∞）内没有零点．

已知函数f（x）=alnx-x（a＞0）．
（Ⅰ）求函数f（x）的最大值；
（Ⅱ）若x∈（0，a），证明：f（a+x）＞f（a-x）；
（Ⅲ）若α，β∈（0，+∞），f（α）=f（β），且α＜β，证明：α+β＞2α

已知F₁、F₂分别是双曲线C₁：

=1（a＞0，b＞0）的左右焦点，且F₂是抛物线C₂：y²=2px（p＞0）的焦点，双曲线C₁与抛物线C₂的一个公共点是P，若线段PF₂的中垂线恰好经过焦点F₁，则双曲线C₁的离心率是（　　）

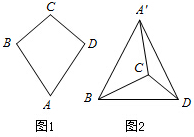如图1，已知四边形ABCD的对角线AC与BD互相垂直，∠A=60°，∠C=90°，CD=CB=2，将△ABD沿BD折起，得到三棱锥A′-BCD，如图2．
（1）若二面角A′-BD-C的余弦值为

，求证：A′C⊥平面BCD；
（2）当三棱锥A′-BCD的体积最大时，求直线A′D与平面A′BC所成角的正弦值．

在△ABC中，若a=2，b+c=7，cosB=-

，求△ABC的面积．

试题分类