题目内容
6．已知函数f（x）=x+$\frac{a}{x}$在区间[1，+∞）上递增，则实数a的取值范围为（ ）| A． | （0，+∞） | B． | （-∞，0） | C． | （0，1] | D． | （-∞，1] |
分析 通过求导得到a≤x2在[1，+∞）恒成立，求出g（x）=x2的最小值，从而求出a的范围．
解答 解：∵f′（x）=1-$\frac{a}{{x}^{2}}$=$\frac{{x}^{2}-a}{{x}^{2}}$≥0在区间[1，+∞）恒成立，
∴x2-a≥0在[1，+∞）恒成立，
∴a≤x2在[1，+∞）恒成立，
令g（x）=x2，x∈[1，+∞），
∴g（x）最小值=1，
∴a≤1，
故选：D．
点评 本题考查了函数的单调性，考查了函数的最值问题，考查转化思想，是一道基础题．
练习册系列答案
相关题目
14．已知二次函数f（x）=2x2-（a-2）x-2a2-a，若在区间[0，1]内至少存在一个实数b，使f（b）＞0，则实数a的取值范围是（ ）
| A． | （-2，1） | B． | $（-\frac{1}{2}，\;2）$ | C． | $（-2，\;-\frac{1}{2}）$ | D． | $（-\frac{1}{2}，\;1）$ |
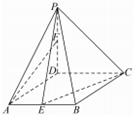如图，在四棱锥P-ABCD中，∠BCD=60°，PD⊥平面ABCD，PD=AD=CD=1，点E、F分别为AB和PD的中点．