题目内容
14.设二次函数f(x)=x2+ax+b(a、b∈R).(1)当b=1时,求函数f(x)在[-1,1]上的值域;
(2)若方程f(x)=0有两个非整数实根,且这两实数根在相邻两整数之间,试证明存在整数k,使得$|{f(k)}|≤\frac{1}{4}$.
分析 (1)求出二次函数的对称轴方程,讨论对称轴和区间[-1,1]的关系,求出函数的最值即可;
(2)设m<x1<x2<m+1,m为整数.分类讨论k的存在性,综合讨论结果,可得答案.
解答 解:(1)当b=1时,f(x)=(x+$\frac{a}{2}$)2+1-$\frac{{a}^{2}}{4}$,对称轴为x=-$\frac{a}{2}$,
当a≤-2时,函数f(x)在[-1,1]上递减,则函数的最大值为:f(-1)=-a;最小值为:f(1)=a.
函数f(x)在[-1,1]上的值域:[a,-a].
当0<a≤2时,即有-1≤-$\frac{a}{2}$<0,函数的最小值:f(-$\frac{a}{2}$)=1-$\frac{{a}^{2}}{4}$;最大值为:f(1)=2+a.
函数f(x)在[-1,1]上的值域:[1-$\frac{{a}^{2}}{4}$,2-a].
当-2<a≤0时,0≤-$\frac{a}{2}$<1,函数f(x)的最小值为:f(-$\frac{a}{2}$)=1-$\frac{{a}^{2}}{4}$;最大值为:f(-1)=2-a.
函数f(x)在[-1,1]上的值域:[1-$\frac{{a}^{2}}{4}$,2+a].
当a>2时,$-\frac{a}{2}$<-1,函数f(x)在[-1,1]上递减,
则函数的最小值为:f(-1)=-a;最大值为:f(1)=a.
函数f(x)在[-1,1]上的值域:[-a,a].…(6分)
(2)设m<x1<x2<m+1,m为整数.
则△=a2-4b>0,即b<$\frac{{a}^{2}}{4}$,
①当-$\frac{a}{2}$∈(m,m+$\frac{1}{2}$],即-1≤a+2m<0时,
f(m)=m2+am+b<m2+am+$\frac{{a}^{2}}{4}$=(m+$\frac{a}{2}$)2≤$\frac{1}{4}$;
②当-$\frac{a}{2}$∈(m+$\frac{1}{2}$,m+1),即-2<a+2m<-1时,
f(m+1)=(m+1)2+a(m+1)+b<(m+2)2+a(m+1)+$\frac{{a}^{2}}{4}$=(m+1+$\frac{a}{2}$)2≤$\frac{1}{4}$;
综上,存在整数k,使得|f(k)|≤$\frac{1}{4}$.…(12分)
点评 本题考查的知识点是二次函数的图象和性质,分类讨论思想,熟练掌握二次函数的图象和性质,是解答的关键.

 特高级教师点拨系列答案
特高级教师点拨系列答案| A. | y=3x | B. | y=2x(-1≤x<1) | ||
| C. | $y=\left\{\begin{array}{l}{x^2}+x,x>0\\{x^2}-x,x<0\end{array}\right.$ | D. | y=2x-2-x |
| 房41017 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.3 |
| B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8. | 3.9 | 4.3 | 4.4 | 4.1 | 4.2 | 4.3 | 4.5 |
(Ⅱ)该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号,每位购房者只有一次抽签机会.
小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格.为了使其购房成功的概率更大,他应该选择哪一种户型抽签?
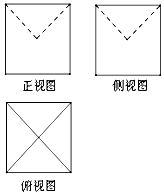 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )| A. | $8-\frac{π}{3}$ | B. | $8-\frac{π}{6}$ | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
| A. | (0,+∞) | B. | (-∞,0) | C. | (0,1] | D. | (-∞,1] |