题目内容
5.f(x)=|sinx|+|cosx|,则f(x)的最小正周期是$\frac{π}{2}$.分析 化简函数f(x)=$\sqrt{1+|sin2x|}$,利用sin2x的周期性求出f(x)的最小正周期.
解答 解:∵函数f(x)=|sinx|+|cosx|
=$\sqrt{{sin}^{2}x{+cos}^{2}x+2|sinx|•|cosx|}$
=$\sqrt{1+|sin2x|}$,
且|sin2x|的最小正周期为$\frac{π}{2}$,
∴f(x)的最小正周期为T=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题主要考查了三角函数恒等变换的应用以及三角函数的周期性问题,是基础题目.

练习册系列答案
相关题目
10.已知等比数列{an}的公比为q=-$\frac{1}{2}$.
(1)若a4=$\frac{1}{8}$,求数列{an}的前n项和;
(2)证明:对任意k∈N*,ak+2是ak与ak+1的等差中项.
(1)若a4=$\frac{1}{8}$,求数列{an}的前n项和;
(2)证明:对任意k∈N*,ak+2是ak与ak+1的等差中项.
17.设函数y=log2$\frac{3}{x-1}$的定义域为集合A,函数y=$\root{3}{x-2}$的定义域为集合B,则A∩B为( )
| A. | {x|x≥2} | B. | {x|x≠1} | C. | {x|x>2} | D. | {x|x>1} |
9.如图,在平面四边形ABCD中,AB=1,$BC=\sqrt{3}+1$,$AD=\sqrt{6}$,∠ABC=120°,∠DAB=75°,则CD=( )
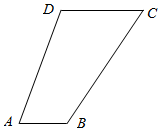

| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{2}+1$ |
10.已知直线l:kx+y-2=0(k∈R)是圆C:x2+y2-6x+2y+9=0的对称轴,过点A(0,k)作圆C的一条切线,切点为B,则线段AB的长为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{3}$ |