题目内容
函数f（x）=ex-x在[-1，1]上的最小值是 ．
考点：利用导数求闭区间上函数的最值
专题：计算题,导数的概念及应用
分析：利用导数求得函数的极值，根据单调性可判断也为最值．
解答：
解：f′（x）=ex-1，
令f′（x）=0，得x=0，
当x∈[-1，0）时，f′（x）＜0，f（x）递减；
当x∈（0，1]时，f′（x）＞0，f（x）递增．
∴x=0时f（x）取得极小值也为最小值，f（0）=1，
故答案为：1．
令f′（x）=0，得x=0，
当x∈[-1，0）时，f′（x）＜0，f（x）递减；
当x∈（0，1]时，f′（x）＞0，f（x）递增．
∴x=0时f（x）取得极小值也为最小值，f（0）=1，
故答案为：1．
点评：该题考查利用导数研究函数的最值，属基础题．
练习册系列答案
相关题目
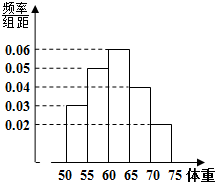某公司为了了解员工们的健康状况，随机抽取了部分员工作为样本，测量他们的体重（单位：公斤），体重的分组区间为[50，55），[55，60），[60，65），[65，70），[70，75]，由此得到样本的频率分布直方图，如图所示．根据频率分布直方图，估计该公司员工体重的众数是一个树表的生长过程依据图中所示的生长规律，则第15行的实心圆的个数是（ ）
| A、68 | B、233 |
| C、377 | D、610 |