题目内容
求导函数:y=
-2.
| sinx |
| x |
考点:导数的运算
专题:导数的概念及应用
分析:根据求导法则和基本初等函数的求导公式求解即可.
解答:
解:由题意得,y′=(
-2)′=(
)′
=
=
.
| sinx |
| x |
| sinx |
| x |
=
| (sinx)′x-(x)′sinx |
| x2 |
| xcosx-sinx |
| x2 |
点评:本题考查求导法则和基本初等函数的求导公式,熟练掌握公式和法则是解题的关键.

练习册系列答案
相关题目
已知全集为U=R,M={x|x2-x>0},N={x|
<0},则有( )
| x-1 |
| x |
| A、M∪N=R |
| B、M∩N=∅ |
| C、∁UN=M |
| D、∁UN⊆N |
设f(x)=Aisn(ωx+φ),?x1,x2∈R,使f(x1)-f(x2)取得最大值2时,|x1-x2|最小值为π,若f(x)在(
,
)上单调递增,在(
,
)上单调递减,则f(-
)等于( )
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 8π |
| 3 |
| A、-2 | B、-1 | C、0 | D、1 |
已知函数f(x)=|logax|-(
)x(a>0且a≠1)有两个零点x1、x2,则有( )
| 1 |
| 2 |
| A、0<x1x2<1 |
| B、x1x2=1 |
| C、x1x2>1 |
| D、x1x2的范围不确定 |
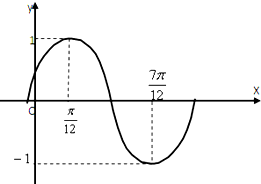 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<