题目内容
9.已知集合Q={(x,y)|$\left\{\begin{array}{l}{y≤x}\\{y-1≥0}\\{x+y-4≤0}\end{array}\right.$},P={(x,y)|x2=2py,p>0},若P∩Q≠∅,则p的最小值为( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 作出P中的简单线性规划,画出P中的抛物线,根据P与Q交集即为空集,确定出p的最小值即可.
解答  解:作出Q中$\left\{\begin{array}{l}{y≤x}\\{y-1≥0}\\{x+y-4≤0}\end{array}\right.$的简单线性规划,如图中阴影部分,作出P中x2=2py,p>0的图象,
解:作出Q中$\left\{\begin{array}{l}{y≤x}\\{y-1≥0}\\{x+y-4≤0}\end{array}\right.$的简单线性规划,如图中阴影部分,作出P中x2=2py,p>0的图象,
当P∩Q≠∅,即x2=2py图象过(1,1)时,p取得最小值,
把(1,1)代入得:1=2p,即p=$\frac{1}{2}$,
则p的最小值为$\frac{1}{2}$,
故选:C.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
17.复数Z=$\frac{3-i}{i-1}$在复平面上所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.设Sn为等比数列{an}的 前n项和,a2-8a5=0,则$\frac{{S}_{8}}{{S}_{4}}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{17}{16}$ | C. | 2 | D. | 17 |
14.已知直线l与平面α相交但不垂直,m为空间内一条直线,则下列结论可能成立的是( )
| A. | m∥l,m⊥α | B. | m∥l,m∥α | C. | m⊥l,m⊥α | D. | m⊥l,m∥α |
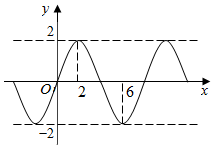 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f (1)+f (2)+f (3)+…f (2015)=0.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f (1)+f (2)+f (3)+…f (2015)=0. 函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则ω=2,φ=$\frac{π}{6}$.
函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则ω=2,φ=$\frac{π}{6}$.