题目内容
1.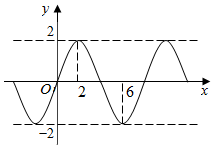 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f (1)+f (2)+f (3)+…f (2015)=0.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f (1)+f (2)+f (3)+…f (2015)=0.
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,克的函数的解析式;再利用利用周期性求得要求的式子的值.
解答 解:函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象,
可得A=2,$\frac{1}{2}$•$\frac{2π}{ω}$=6-2,∴ω=$\frac{π}{4}$.
再根据图象经过原点,可得φ=0,∴f(x)=2sin$\frac{π}{4}$x.
由于f(x)的周期为$\frac{2π}{\frac{π}{4}}$=8,f (1)+f (2)+f (3)+…f (8)=0,
则f (1)+f (2)+f (3)+…f (2015)=251×0+f (1)+f (2)+f (3)+…f (7)
=0,
故答案为:0.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,利用周期性求函数的值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.(x2-3)($\frac{1}{{x}^{2}}$+1)5的展开式的常数项是( )
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
9.已知集合Q={(x,y)|$\left\{\begin{array}{l}{y≤x}\\{y-1≥0}\\{x+y-4≤0}\end{array}\right.$},P={(x,y)|x2=2py,p>0},若P∩Q≠∅,则p的最小值为( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
13.已知集合A={x∈z|-2≤x<3},B={x|-2≤x<1},则A∩B=( )
| A. | {-2,-1,0} | B. | {-2,-1,0,1} | C. | {x|-2<x<1} | D. | {x|-2≤x<1} |
10.记集合A={x|x-a>0},B={y|y=sinx,x∈R},若0∈A∩B,则a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,0] | C. | [0,+∞) | D. | (0,+∞) |
 如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c):
如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c):


