题目内容
17．复数Z=$\frac{3-i}{i-1}$在复平面上所对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数的运算性质、几何意义即可得出．
解答 解：复数Z=$\frac{3-i}{i-1}$=$\frac{（i-3）（1+i）}{（1-i）（1+i）}$=$\frac{-4-2i}{2}$=-2-i在复平面上所对应的点（-2，-1）位于第三象限．
故选：C．
点评 本题考查了复数的运算性质、几何意义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
智慧小复习系列答案
相关题目
7．已知A，B为双曲线E的左、右顶点，C为E上的一点，若A，B，C三点构成顶角为120°的等腰三角形，则E的离心率为（ ）
| A． | $\frac{1+\sqrt{3}}{2}$ | B． | $\sqrt{\frac{8\sqrt{3}-9}{3}}$ | C． | $\sqrt{2}$ | D． | 2 |
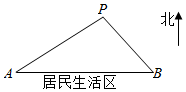如图所示，A，B是两个垃圾中转站，B在A的正东方向16千米处，AB的南面为居民生活区，为了妥善处理生活垃圾，政府决定在AB的背面建一个垃圾发电厂P，垃圾发电厂P的选址拟满足以下两个要求（A，B，P可看成三个点）：
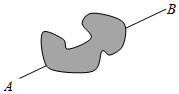如图所示，为了测量某湖泊两侧A，B间的距离，李宁同学首先选定了与A，B不共线的一点C，然后给出了三种测量方案：（△ABC的角A，B，C所对的边分别记为a，b，c）：
9．已知集合Q={（x，y）|$\left\{\begin{array}{l}{y≤x}\\{y-1≥0}\\{x+y-4≤0}\end{array}\right.$}，P={（x，y）|x2=2py，p＞0}，若P∩Q≠∅，则p的最小值为（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
7．“$θ=2kπ+\frac{π}{4}（k∈Z）$”是“tanθ=1”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |