题目内容
19.已知a∈R,直线l1:(2a+1)x+2y-a+2=0与直线l2:2x-3ay-3a-5=0垂直.(1)求a的值;
(2)求以l1,l2的交点为圆心,且与直线3x-4y+9=0相切的圆的方程.
分析 (1)利用两条直线斜率的积为-1,建立方程,即可求a的值;
(2)联立l1,l2的方程,得到交点为圆心,求出圆心与直线3x-4y+9=0的距离,可得半径,即可求出圆的方程.
解答 解:(1)直线l1的斜率为k1=$-\frac{2a+1}{2}$,…(1分)
当a=0时,直线l2与x轴垂直,显然不与直线l1垂直,
∴a≠0,∴直线l2的斜率为k2=$\frac{2}{3a}$…(3分)
∵l1⊥l2,∴k1×k2=-1…(4分)
即$-\frac{2a+1}{2}$×$\frac{2}{3a}$=-1,解得a=1…(6分)
(2)由(1)知,l1:3x+2y+1=0,l2:2x-3y-8=0
以上二方程联立$\left\{\begin{array}{l}3x+2y+1=0\\ 2x-3y-8=0\end{array}\right.$,解得$\left\{\begin{array}{l}x=1\\ y=-2\end{array}\right.$,即圆心坐标为(1,-2)…(8分)
圆心到直线3x-4y+9=0的距离为$\frac{{|3×1-4×({-2})+9|}}{{\sqrt{{3^2}+{{({-4})}^2}}}}=4$…(10分)
∴圆的半径为4 …(11分)
∴所求圆的方程为(x-1)2+(y+2)2=42…(12分)
点评 本题考查直线与直线的位置关系,考查圆的方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
9.已知点A(-1,2),B(2,3),直线l:kx-y-k+1=0与线段AB相交,则实数k的取值范围是( )
| A. | -$\frac{1}{2}$≤k≤2 | B. | k≤-$\frac{1}{2}$或k≥2 | C. | -2≤k≤$\frac{1}{2}$ | D. | k≤-2或k≥$\frac{1}{2}$ |
10.已知函数f(x)=x•cosx,则$f'({\frac{π}{2}})$的值为( )
| A. | $-\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | 1 | D. | -1 |
7.如图,正六边形ABCDEF中,$\overrightarrow{BC}$$+\overrightarrow{DE}$$+\overrightarrow{AF}$等于( )
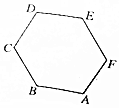

| A. | $\overrightarrow{EB}$ | B. | $\overrightarrow{BE}$ | C. | $\overrightarrow{AD}$ | D. | $\overrightarrow{CF}$ |
14.函数$f(x)=\frac{1}{x}$的导数是( )
| A. | $\frac{1}{x^2}$ | B. | $-\frac{1}{x^2}$ | C. | $\frac{1}{2x}$ | D. | $-\frac{1}{2x}$ |
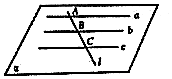
 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,PA=AD,E、F分别是棱PD、BC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,PA=AD,E、F分别是棱PD、BC的中点.